玻意耳-马略特定律
波义耳定律(又称马里奥特定律、波义耳-马里奥特定律)是关于理想气体的定律。
该法可说明如下:
换句话说,恒定质量的理想气体在恒定温度下的体积与施加在它身上的压力成反比。
在符号中,法律是。
P ∝ 1 V {\displaystyle P\propto {\frac {1}{V}}}.
或
P V = k {\displaystyle PV=k}。
对于给定质量的气体,在恒温下,压强和体积的乘积是一个常数。当体积减小时,压强会按比例增加,反之亦然。例如,当压强减半时,体积增加一倍。
假设你有一个罐子,在一定压力下装有一定体积的气体。当你减小罐子的体积时,同样数量的气体颗粒现在被装在一个较小的空间里。因此,碰撞的次数就会增加。因此,压力更大。
想象一下,你有一个气体在一定的压力(P1)和体积(V1)。如果你把压力改变到一个新的值(P2),体积就会改变到一个新的值(V2)。我们可以用波义耳定律来描述这两组条件。
P 1 V 1 = k {displaystyle P_{1}V_{1}=k}.
P 2 V 2 = k {displaystyle P_{2}V_{2}=k}.
常数k在两种情况下都是一样的,所以我们可以这样说。
P 1 V 1 = P 2 V 2 {\displaystyle P_{1}V_{1}=P_{2}V_{2}}}。
例子:一个气体的压力是3大气压,体积是5升。一种气体的压力是3大气压,体积是5升。如果压力降低到2个大气压,体积是多少?
P 1 V 1 = P 2 V 2 {\displaystyle P_{1}V_{1}=P_{2}V_{2}}}。
V 2 = P 1 V 1 P 2 {\displaystyle V_{2}={\frac {P_{1}V_{1}}}{P_{2}}}}。
V 2 = 3 ∗ 5 2 {\displaystyle V_{2}={/frac {3*5}{2}}}。
V 2 = 15 2 {\displaystyle V_{2}={\frac {15}{2}}}}。
V 2 = 7.5 {displaystyle V_{2}=7.5}。
∴容积为7.5升。
该法由罗伯特-博伊尔于1662年发现,之后由埃德姆-马里奥特于1679年独立发现。
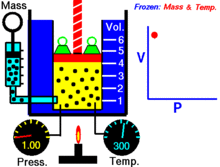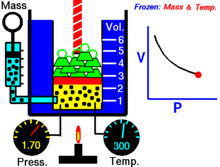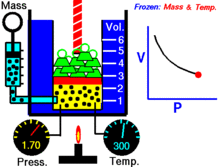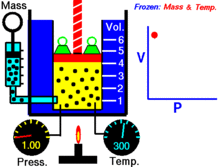
展示压强和体积关系的动画.气体的量和温度是不变的。
问题和答案
问:什么是波义耳定律?答:波义耳定律(又称马里奥特定律和波义耳-马里奥特定律)是一条关于理想气体的定律,它指出,对于保持恒温的固定数量的理想气体,其压力(P)和体积(V)成反比。
问:我们如何用数学方法表达波义耳定律?
答:我们可以将波义耳定律在数学上表示为P∝1/V或PV=k,其中P是气体的压力,V是气体的体积,而k是一个常数。
问:谁发现了这个定律?
答:这个定律是由罗伯特-波义耳在1662年发现的,之后由埃德蒙-马里奥特在1679年独立发现。
问:当我们说P和V成反比时是什么意思?
答:这意味着,当其中一个增加时,另一个就会按比例减少--因此,如果你在一定的压力下减少装有一定量气体的罐子的体积,那么,由于在较小的空间内,粒子之间的碰撞增加,压力就会增加。
问:我们如何使用波义耳定律来计算压力或体积的变化?
答:我们可以使用波义耳定律来计算压力或体积的变化,方法是使用两个方程式--P1V1=k和P2V2=k--其中k保持不变,而P1/V1或P2/V2则根据你要计算的内容而变化。
问:我们也可以将这一定律应用于实际气体吗?
答:不能--这只适用于理想气体,因为它们之间没有分子间力。
搜索百科全书








