絕妙定理
高斯的Theorema Egregium(拉丁文是 "显著定理")是卡尔-弗里德里希-高斯证明的微分几何学的一个重要成果。该定理是关于曲面的曲率。该定理指出,仅通过测量曲面上的角度、距离和它们的速率就可以确定曲率。不需要谈及曲面嵌入周围三维欧几里得空间的特殊方式。换句话说,如果人们在不拉伸表面的情况下弯曲表面,其高斯曲率是不会改变的。
高斯以这种方式提出了该定理(从拉丁文翻译过来)。
由于这个原因,前文中的公式本身导致了一个非凡的定理。如果一个弯曲的表面在任何其他的表面上发展,每一个点的曲率测量都保持不变。
这个定理是 "了不起的",因为高斯曲率的起始定义直接利用了曲面在空间的位置。因此,尽管经历了所有的弯曲和扭曲变形,这个结果并不取决于它的嵌入,这是相当令人惊讶的。
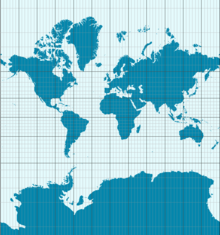
Theorema Egregium的一个后果是,地球在地图上显示时不能不变形。这里显示的墨卡托投影,保留了角度,但改变了面积。例如,南极洲被显示得比它的实际面积大得多。
问题和答案
问:高斯的 "Egregium理论 "是什么?答:高斯的Egregium定理是微分几何学中关于曲面曲率的一个重要结果,由卡尔-弗里德里希-高斯证明。
问: 根据高斯的Egregium定理, 如何确定曲率?
答:根据高斯的 "Egregium定理",曲率可以通过测量曲面上的角度、距离及其比率来确定。
问: 是否有必要讨论曲面嵌入周围三维欧几里得空间的特定方式来确定曲率?
答:不需要,根据高斯的Egregium定理,不需要讨论曲面嵌入周围三维欧几里得空间的特定方式来确定曲率。
问:如果不拉伸曲面而将其弯曲,曲面的高斯曲率会改变吗?
答:不会,根据高斯Egregium定理,如果不拉伸曲面而将其弯曲,曲面的高斯曲率不会改变。
问:是谁以这种方式提出这个定理的?
答:高斯以这种方式提出了该定理。
问:这个定理有什么了不起的地方?
答: 这个定理之所以 "了不起",是因为高斯曲率的起始定义直接使用了曲面在空间的位置。因此,令人惊讶的是,尽管经历了所有的弯曲和扭曲变形,该结果并不依赖于其嵌入。
问:高斯是如何提出这个定理的?
答:高斯是这样提出这个定理的:如果一个曲面在任何其他曲面上展开,那么每个点的曲率都保持不变。
搜索百科全书