歐拉﹣伯努力棟樑方程
欧拉-伯努利梁理论（也被称为工程师的梁理论或经典梁理论）是一种简单的方法，用于计算施加载荷时梁的弯曲。这适用于梁的小挠度（东西移动的程度），而不考虑剪切变形的影响。因此，它可以被认为是季莫申科梁理论的一个特例。它最早是在1750年左右提出的。它在19世纪末埃菲尔铁塔和摩天轮的发展过程中得到了普及。此后，它被用于许多工程领域，包括机械工程和土木工程。尽管其他先进的方法已经被开发出来，欧拉-伯努利梁理论由于其简单性仍然被广泛使用。
一个振动的玻璃梁显示了梁的弯曲，可以用欧拉-伯努利的梁理论来估计。
历史
莱昂哈德-欧拉和丹尼尔-伯努利于1750年首次将这一理论整理出来。在当时，人们对科学和工程的看法与今天不同。像欧拉-伯努利梁理论这样的数学理论在实际工程使用中不被信任。桥梁和建筑继续使用相同的方法进行设计，直到19世纪末。这时埃菲尔铁塔和摩天轮在更大范围内显示了理论的有效性。
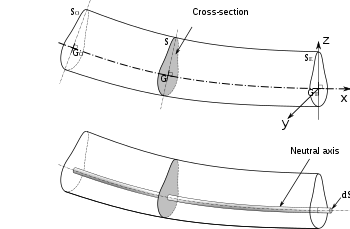
显示中性轴的弯曲梁横截面图
静态梁方程
欧拉-伯努利方程描述了梁的挠度和施加的载荷之间的关系，如下所示。
d 2 d x 2 ( E I d 2 w d x 2 ) = q {displaystyle {frac {mathrm {d}} {mathrm {d}} ^{2}}}\left(EI{frac {mathrm {d}} ^{2}w}{mathrm {d}}})^{2}}{mathrm {d}x^{2}}}左(EI{frac {mathrm {d} ^{2}w}{mathrm {d} x^{2}}}右)=q\,}。 
其中w ( x ) {displaystyle w(x)}描述
了梁在某个位置x {displaystyle z}
方向的挠度
。q {displaystyle q}
是一个分布载荷，换句话说，是每单位长度的力（类似于压力是每面积的力）；它可能是x {displaystyle x}、w {displaystyle w}的函数。
或其他变量的函数。
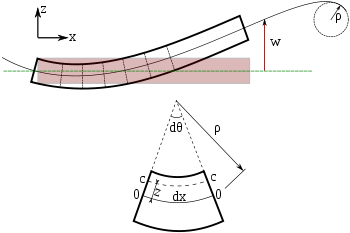
欧拉-伯努利梁的弯曲。梁的每个横截面与中性轴成90度。
问题和答案
问：什么是欧拉-伯努利梁理论？答：欧拉-伯努利梁理论是一种简单的方法，用于计算施加载荷时梁的弯曲，不考虑剪切变形的影响。
问：欧拉-伯努利梁理论何时首次提出？
答：欧拉-伯努利梁理论最早是在1750年左右提出的。
问：欧拉-伯努利梁理论是否用于埃菲尔铁塔和摩天轮的开发？
答：是的，欧拉-伯努利梁理论在19世纪末埃菲尔铁塔和摩天轮的发展中得到了普及。
问：欧拉-伯努利梁理论在哪些工程领域得到了应用？
答：欧拉-伯努利梁理论已被应用于许多工程领域，包括机械工程和土木工程。
问：欧拉-伯努利梁理论今天还在广泛使用吗？
答：是的，欧拉-伯努利梁理论由于其简单性，今天仍然被广泛使用，尽管其他先进的方法已经被开发出来。
问：欧拉-伯努利梁理论适用于哪些类型的梁的挠度？
答：欧拉-伯努利梁理论适用于梁的小挠度。
问：欧拉-伯努利梁理论是否考虑到剪切变形的影响？
答：不，欧拉-伯努利梁理论不考虑剪切变形的影响。
