不等
不平等是指当一个物体是。
- 小于其他(a < b {\displaystyle \<b}表示
a小于b)。
- 大于其他(a>b {\displaystyle \a>b}表示
a大于b)。
- 不小于其他(a≥b {\displaystyle a\geq b
}表示a不小于b,即它要么大于,要么等于b)。
- 不大于其他(a≤b {\displaystyle a\leq b}
表示a不大于b,或者它小于或等于b)。
不等式有时用来命名一个表达式比另一个表达式小、大、不小或不大的说法。
处理不平等问题
数学中的不等式是指两种解法或答案比较时大于或小于。它是指两个或多个解被比较的数量不相等。解不等式就是要找到它的解。当你把一个数字代入一个变量,并且声明为真,那么它就是一个解。当你把一个数字代入一个变量,而语句不为真时,那么这个数字就不是语句的解。
不等式是为一个给定的变量找一个解。它是寻找一个集合的相对顺序。不等式有很多解,但你需要找到实数解。不等式就是求实数的解。不等式的正确读法是从左到右,就像其他方程一样,但唯一不同的是它们对每个方程都有不同的规则。
例如:x+4>12,其中x为实数。首先,一个人需要找到x,他/她需要知道它是否是一个解决方案。答案就会是x>8,这是一个真言。这个表达式是关于x在实数集合中的位置。数字线是显示相对于所有其他实数的位置的一种方法(见图中不等式1)。
.jpg)
不等式1 这是方程x+4>12的解。
不同种类的不等式
有五种不同的不平等。
- 第一个是线性不等式,线性不等式是一种不等式,它是以小于或等于、小于或大于、大于的方式来区分表达式。它是如果我们把不等式换成等量关系,那么结果就是一个线性方程。
- 第二个是不等式的组合,不等式要满足不等式,你必须在解集里有一个数,所以满足不等式的数要在两个解集的交叉处取值。
- 第三种是涉及绝对值的不等式,也就是可以把数值改写成不等式的组合,将涉及绝对值。
- 第四种叫多项式不等式的意思是说它是连续的,就是指它们的图形没有任何跳跃或断裂。
- 最后但并非最不重要的,是有理不等式,这意味着它是多项式除以多项式的形式之一。换句话说,有理函数图没有任何断点,也不在分母的零点处表示。
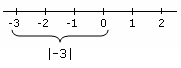
绝对值 显示绝对值的例子
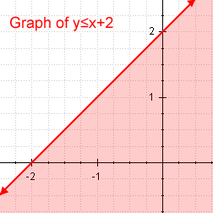
线性 不等式 线性不等式的例子
解不等式的四种方法
二次方程的解法有四种。
- 规则一是你必须在两边加减相同的数字。
- 规则二是要移位,改变不等式的符号定位。
- 规则三是你必须要乘法。
- 法则四是将同一个正数或负数的两边相除。但是,这些只能用在简单的不等式问题上。
另外,解一个不等式要分两步走。第一个是用加法或减法的倒数来简化。第二种是用乘法或除法的倒数来简化更多。当你在用负数乘或除的时候,记得把不等式的符号转过来。

加不等式的例子。

不等式的乘法示例
解不等式的例子
不等式是一种数学陈述,它解释了两个值不相等和不同。不等式ab表示a不等于b。不等式与任何等式都是一样的,但唯一不同的是不等式不使用等号,而是使用符号。不等式b>a表示b大于a,限速、标志等都用不等式来表示。
当解一个不等式时,一个人需要有一个真实的陈述。当你把一个不等式的两边都是负数的时候,这个不等式的陈述是错误的.为了使负数的陈述正确,你需要把符号反过来才能使这个陈述正确.当一个数字是正数时,你不需要将符号倒过来。不等式就是要做出一个真实的陈述。
例如,从一个真语句-6y<-12开始。当两边都除以-6时,结果将变成y<2.在这个语句中,需要将符号反过来才能有真语句,y>2是正确答案。在数线中(见图不等式2),封闭的阴影圈指出它是包含在解集中的.一个开放的圆圈指出它不包括在解集中.
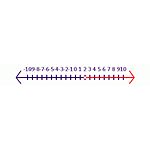
不等式2 方程-6y<-12的解法
相关网页
- 平等性
- 等式
问题和答案
问:"a答:是指a小于b。问:"a > b "是什么意思?
答:意思是a比b大。
问:"a≥b "是什么意思?
答:意思是a不比b小,也就是说,它要么比b大,要么等于b。
问:"a≤b "是什么意思?
答:意思是a不比b大,或者它小于或等于b。
问:数学中如何使用不等式?
答:不等式可以用来命名一种说法,即一个表达式比另一个表达式小、大、不小或不大。
搜索百科全书