線性回歸
线性回归是用一条直线来解释一个因变量和一个或多个解释变量之间关系的方法。它是回归分析的一种特殊情况。
线性回归是第一个被严格研究的回归分析类型。这是因为与未知参数呈线性关系的模型比与其参数呈非线性关系的模型更容易拟合。更重要的是，由此产生的估计器的统计特性更容易确定。
线性回归有许多实际用途。大多数应用属于以下两大类之一：
- 线性回归可用于将一个预测模型拟合到一组观察值（数据）上。如果目标是预测，或预测，或减少，这很有用。在建立这样一个模型后，如果再给出一个X的附加值，而不附带y的值，则可使用拟合模型对y的值进行预测。
- 给定一个变量y和一些可能与y相关的变量X1，...，Xp，可以应用线性回归分析来量化y与Xj之间的关系强度，评估哪些Xj与y完全没有关系，并确定Xj的哪些子集包含y的冗余信息。
线性回归模型尽量使线与数据点（如残差）之间的垂直距离尽可能小。这就是所谓的"线与数据的拟合"。通常情况下，线性回归模型试图使残差的平方和最小化（最小二乘法），但也存在其他拟合方式。它们包括最小化其他一些规范中的"拟合度不足"（如最小绝对偏差回归），或最小化最小二乘损失函数的惩罚版本，如岭回归。最小二乘法也可用于拟合非线性的模型。如上所述，"最小二乘法"和"线性模型"这两个词密切相关，但它们不是同义词。
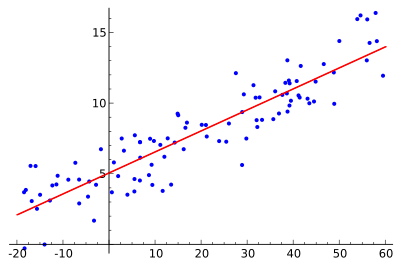
我们的想法是找到红色的曲线，蓝色的点是实际的样本。通过线性回归，所有的点都可以用一条直线连接。这个例子使用简单的线性回归，红线和每个样本点之间的距离的平方是最小的。
问题和答案
问：什么是线性回归？答：线性回归是用数学的方法来研究当其他事物发生变化时，某事物如何变化。它使用一个因变量和一个或多个解释变量来创建一条直线，称为 "回归线"。
问：线性回归的优点是什么？
答：对其未知参数有线性依赖的模型比对其参数有非线性依赖的模型更容易拟合。此外，由此产生的估计器的统计特性更容易确定。
问：线性回归的一些实际用途是什么？
答：线性回归可用于将预测模型与观察值（数据）进行拟合，以便进行预测、预报或还原。它还可以用来量化变量之间的关系强度，并确定包含另一个变量的冗余信息的数据子集。
问：线性回归模型如何试图使误差最小化？
答：线性回归模型试图使直线和数据点之间的垂直距离（残差）尽可能小。这是通过最小化残差的平方之和（最小二乘法）、在某些其他准则中缺乏拟合（最小绝对偏差）或最小化最小二乘法损失函数的惩罚版本（岭回归）来实现的。
问：线性回归模型有可能不基于最小二乘法吗？
答：是的，线性回归模型有可能不以最小二乘法为基础，而是使用诸如最小化其他准则中的不适合（最小绝对偏差）或最小化最小二乘损失函数的惩罚版本（山脊回归）的方法。
问："线性模型 "和 "最小二乘法 "是同义词吗？
答：不，它们不是同义词。虽然它们密切相关，但 "线性模型 "特指使用直线，而 "最小二乘法 "特指通过确保直线和数据点之间有最小的垂直距离来尝试最小化误差。
