单位圆
在数学中，单位圆是一个半径为1的圆，单位圆的方程是x +2 y = {21displaystyle x^{2}+y^{2}=1}
。单位圆以原点为中心，即坐标（0,0）。它经常被用于三角学中。
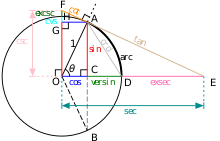
单位圆可以用来建立每个三角函数的模型。
单位圆内的三角函数
在一个单位圆中，t {displaystyle t}
是所需的角度，x {displaystyle x}
和y {displaystyle y}
可以定义为cos ( t ) = x {displaystyle cos(t)=x}
，sin ( t ) = y {displaystyle sin(t)=y}
。使用单位圆的函数，x +2 y =2 {1displaystyle x^{2}+y^{2}=1}，单位圆的另一个方程。另一个单位圆的方程式被发现，cos (2 t ) + sin (2 t ) = {1displaystyle cos ^{2}(t)+sin ^{2}(t)=1}
。当使用三角函数时，主要是使用0到π之间的角度{2displaystyle pi\over 2}
弧度，或0到90度。然而，也有可能有比这更高的角度。使用单位圆，可以找到两个相同点：cos ( t ) = cos ( 2⋅ π k + t ) {displaystyle cos(t)=\cos(2\cdot \pi k+t)}
和s i n ( t ) = sin ( 2⋅ π k + t ) {\displaystyle sin(t)=sin(2\cdot \pi k+t)}
对于任何整数k {displaystyle k}
。
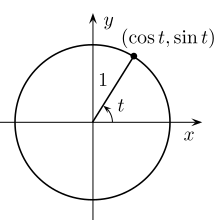
单位圆可以替代三角函数的变量。
问题和答案
问：什么是单位圆？答：单位圆是半径为 1 的圆。
问：什么是单位圆的方程？
答：单位圆的方程是 x^2 + y^2 = 1。
问：单位圆的圆心在哪里？
答：单位圆的圆心是原点，即坐标（0,0）。
问：单位圆在数学中有什么作用？
答：三角函数中经常用到单位圆。
问：为什么单位圆很重要？
答：单位圆之所以重要，是因为它有助于理解角与三角函数之间的关系。
问：单位圆的半径是多少？
答：单位圆的半径是 1。
问：单位圆的半径是 1 有什么意义？
答：单位圆半径为 1 的意义在于它简化了计算，使角度与三角函数值之间的关系变得容易。
