数学

数学是对数字、形状和模式的研究。这个词来自希腊语"μάθημα"（máthema），意思是"科学、知识或学习"，有时也被简称为数学（在英国、澳大利亚、爱尔兰和新西兰）或数学（在美国和加拿大）。学生和学校经常用这些短语来表示算术、几何或简单的代数。

数学包括研究：

数字：事物如何计算。
结构：事物是如何组织起来的。这个子领域通常称为代数。
地点：事物所在的地方及其排列。这个子领域通常称为几何学。
变化：事物如何变得不同。这一分领域通常称为分析。

数学对于解决现实世界中发生的问题是很有用的，所以除了数学家之外，很多人都在研究和使用数学。今天，很多工作都需要一些数学知识。从事商业、科学、工程、建筑的人都需要一些数学知识。

数学中的问题解决

数学是用逻辑来解决问题的。数学家使用的主要逻辑工具之一是演绎法。演绎是一种特殊的思维方式，用旧的真理来发现和证明新的真理。对数学家来说，某件事情为真的原因（称为证明）与它为真的事实同样重要，而这个原因往往是利用演绎法找到的。使用演绎法是数学思维与其他科学思维的不同之处，后者可能依赖于实验或访谈。

逻辑和推理被数学家用来创建一般规则，这是数学的重要组成部分。这些规则省略了不重要的信息，这样一条规则就可以覆盖很多情况。通过找到一般规则，数学可以解决很多问题，同时这些规则也可以用在其他问题上。这些规则可以被称为定理（如果它们已经被证明）或猜想（如果还不知道它们是否为真）。大多数数学家使用非逻辑的和创造性的推理来寻找逻辑证明。

有时候，数学会发现和研究一些我们还不理解的规则或思想。在数学中，往往选择一些想法和规则，因为它们被认为是简单或整齐的。另一方面，有时这些思想和规则在数学中被研究后，在现实世界中被发现，这种情况在过去已经发生过很多次。一般来说，研究数学的规则和思想可以帮助我们更好地理解这个世界。数学问题的一些例子是加、减、乘、除、微积分、分数和小数。代数问题是通过评估某些变量来解决的。计算器在四种基本算术运算中回答每一个数学问题。

数学研究领域

数量

数学包括对数和量的研究，它是科学的一个分支，涉及形状、数量和排列的逻辑。下面列出的大部分领域在许多不同的数学领域都有研究，包括集合论和数学逻辑。数论的研究通常更侧重于整数的结构和行为，而不是数字本身的实际基础，所以不在本小节中列出。

0, 1, 2, 3, ... {\displaystyle 0,1,2,3,\ldots}。 $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , ... {\displaystyle \ldots ,-1,0,1,\ldots }. $\ldots ,-1,0,1,\ldots$	1 2 , 2 3 , 0.125 , ... {\displaystyle {\frac {1}{2}}},{\frac {2}{3}},0.125,\ldots }。 ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\displaystyle \pi ,e,{\sqrt {2}},\ldots }。 $\pi ,e,{\sqrt {2}},\ldots$	1+i , 2 e i π / 3 , ... {\displaystyle 1+i,2e^{i/pi /3},\ldots }。 $1+i,2e^{i\pi /3},\ldots$
自然数	整数	有理数	实数	复数
0,1,...,ω,ω+1,...,2 ω,...{\displaystyle 0,1,ldots ,\omega ,\omega +1,ldots ,2\omega ,ldots }。 $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	↪Lo_2135↩ 0 , ↪Lo_2135↩ 1 , ... {\displaystyle aleph _{0},aleph _{1},\ldots }。 $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ {\displaystyle +,-,\times ,div }。 $+,-,\times ,\div$	> , ≥ , = , ≤ , < {/displaystyle >,\geq ,=,\leq ,< }。 $>,\geq ,=,\leq ,<$	f ( x ) = x {\displaystyle f(x)={\sqrt {x}}}}。 $f(x)={\sqrt {x}}$
序数	主数	算术运算	算术关系	职能

架构

数学的许多领域都在研究对象所具有的结构。这些领域大多是代数研究的一部分。


数字理论	抽象代数	线性代数	秩序论	图论

形状

数学的某些领域研究的是事物的形状。这些领域大多是几何学研究的一部分。


拓扑学	几何学	三角学	微分几何学	分形几何学

变化

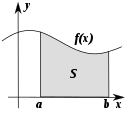
数学的一些领域研究事物的变化方式。这些领域大多是分析研究的一部分。


微积分	矢量微积分	分析报告

微分方程	动力系统	混沌理论

应用数学

应用数学用数学来解决工程、物理、计算机等其他领域的问题。

数值分析--优化--概率论--统计学--数学金融--博弈论--数学物理--流体力学--计算算法

著名定理

这些定理让数学家和不是数学家的人都很感兴趣。

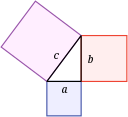
毕达哥拉斯定理--费马最后定理--哥德巴赫猜想--双质数猜想--哥德尔不完备性定理--波恩卡雷猜想--坎托尔对角线论证--四色定理--佐恩定理--欧拉认同--丘奇-图灵论题。

这些都是大大改变了数学的定理和猜想。

黎曼假说--连续假说--P与NP--毕达哥拉斯定理--中心极限定理--微积分基本定理--代数基本定理--算术基本定理--投影几何基本定理--曲面分类定理--高斯-波奈定理--费马最后定理--康托洛维奇定理。

基础和方法

对数学本质认识的进步也影响着数学家对其学科的研究方式。

数学哲学--数学直觉主义--数学建构主义--数学基础--集合论--符号逻辑--模型论--范畴论--逻辑--逆向数学--数学符号表。

历史和数学家的世界

历史上的数学，以及数学史。

数学史 - 数学年表 - 数学家 - 菲尔兹奖章 - 阿贝尔奖 - 千年奖问题（克莱数学奖） - 国际数学联合会 - 数学竞赛 - 横向思维 - 数学和性别

数学方面的奖项

数学界没有诺贝尔奖。数学家可以因重要作品获得阿贝尔奖和菲尔兹奖章。

克雷数学研究所表示，将向任何解决其中一个千年奖问题的人提供100万美元。

数学工具

做数学题或者找数学题的答案，有很多工具都会用到。

旧工具

算盘
纳皮尔的骨头，滑动规则
尺子和指南针
心算

较新的工具

计算器和计算机
编程语言
计算机代数系统(列表)
网络速记
统计分析软件
SAS编程语言
R编程语言

另见

数学界妇女的年表
美国数学会
工业和应用数学学会
数学家谱项目
数学学科分类

问题和答案

问：什么是数学？
答：数学是对数字、形状和模式的研究。这个词来自希腊文μάθημα（máthema），意思是 "科学、知识或学习"。

问：数学的主要领域是什么？
答：数学的主要领域包括数字、结构（代数）、位置（几何）和变化（分析）。

问：数学在现实世界中是如何应用的？
答：应用数学对解决现实世界中的问题很有用。从事商业、科学、工程和建筑工作的人都会用到数学。

问："数学 "是否有一个简短的版本？
答：有的--在英联邦国家可以简称为'maths'，在北美可以简称为'math'。

问："数学 "这个词是什么意思？
答："数学 "一词来自希腊文μάθημα（máthema），意思是 "科学、知识或学习"。

问：应用数学涉及哪类问题的解决？
答：应用数学涉及解决现实世界中从事商业、科学、工程和建筑的人所面临的问题。