杨-拉普拉斯公式
在物理学中,杨-拉普拉斯方程(/ləˈplɑːs/)是一个非线性偏微分方程,它描述了两个静态流体(如水和空气)之间界面的毛细管压力差。这个差值是由于表面张力或壁张力现象造成的。壁张力只能用于非常薄的壁。杨-拉普拉斯方程将压力差与表面或壁的形状联系起来。它在研究静态毛细管表面时非常重要。
在生理学上,它被称为拉普拉斯定律。它被用来描述中空器官内的压力。
该方程是以托马斯-杨(Thomas Young)的名字命名的,他在1805年发展了表面张力的定性理论,而皮埃尔-西蒙-拉普拉斯(Pierre-Simon Laplace)在第二年完成了数学描述。它有时也被称为杨-拉普拉斯-高斯方程。卡尔・弗里德里希・高斯统一的工作 杨和拉普拉斯在1830年。高斯得出的微分方程和边界条件使用约翰-伯努利的虚拟工作原理。
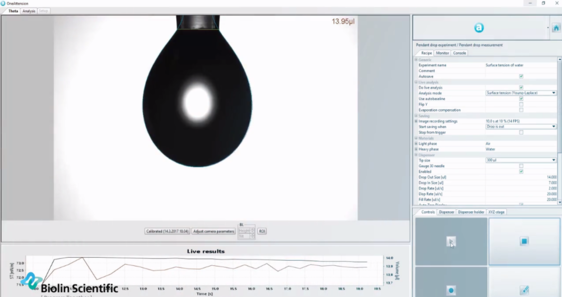
光学张力计利用Young-Laplace方程,根据垂液滴形状自动确定液体表面张力。
问题和答案
问:什么是杨-拉普拉斯方程?答:杨-拉普拉斯方程是一个非线性偏微分方程,描述了两种静态流体(如水和空气)之间界面的毛细管压力差。
问:它与什么有关?
答:它将压力差与表面或墙壁的形状联系起来。
问:谁提出了这一理论?
答:这个理论是由托马斯-杨在1805年提出的,皮埃尔-西蒙-拉普拉斯在第二年完成了它的数学描述。后来由卡尔-弗里德里希-高斯在1830年统一了它。
问:它在生理学中是如何使用的?
答:在生理学上,它被称为拉普拉斯定律,用于描述空心器官内的压力。
问:它能解释什么现象?
答:杨-拉普拉斯方程解释了表面张力或壁张力的现象。
问:壁张力是否适用于厚壁?答:不,壁面张力只适用于非常薄的壁。
搜索百科全书