表面张力
表面张力是一种效果,即液体的表面很强。表面可以托起一个重量,水滴的表面将水滴固定在一起,形成一个球状。一些小东西可以因为表面张力而漂浮在表面上,尽管它们通常不能漂浮。一些昆虫(如水黾)能在水面上奔跑就是因为这个原因。这一特性是由液体中的分子相互吸引(内聚力)造成的,是液体的许多行为的原因。
表面张力的维度是每单位长度的力,或每单位面积的能量。两者是等价的,但是当提到每单位面积的能量时,人们使用表面能这个术语--这是一个更普遍的术语,因为它也适用于固体而不仅仅是液体。
在材料科学中,表面张力被用来表示表面应力或表面自由能。
原因
液体分子之间的内聚力导致表面张力。在液体的主体中,每个分子在每个方向上都被相邻的液体分子平均拉动,导致净力为零。表面的分子没有其他分子在它们的四面,因此被向内拉。这就产生了一些内部压力,迫使液体表面收缩到最小面积。
表面张力是造成液滴形状的原因。虽然容易变形,但水滴往往被表面层的内聚力拉成球形。在没有其他力量,包括重力的情况下,几乎所有液体的水滴都是完全球形的。根据拉普拉斯定律,球形形状将表面层必要的 "壁张力 "降到最低。
另一种方法是用能量来看待它。一个与邻居接触的分子的能量状态比它单独存在(不与邻居接触)的时候要低。内部分子有尽可能多的邻居,但边界分子缺少邻居(与内部分子相比)。所以,边界分子的能量更高。为了使液体的能量状态最小化,必须使高能量的边界分子数量最小化。边界分子数量的最小化导致了表面积的最小化。
作为表面积最小化的结果,一个表面会呈现出它所能达到的最平滑的形状。表面形状中的任何曲率都会导致更大的面积和更高的能量。因此,表面将推回任何曲率,就像一个被推上山的球将推回以减少其重力势能一样。
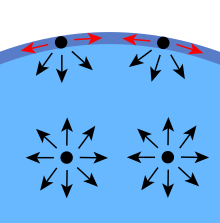
液体中分子的作用力图示

表面张力使回形针不能被淹没。
日常生活中的影响
水
研究水显示了表面张力的几种影响。
A.雨水在蜡质表面上形成珠子,如叶子。水对蜡的附着力很弱,对自身的附着力很强,所以水聚集成了水珠。表面张力使它们形成了近乎球形的形状,因为球形的表面积与体积的比例是最小的。
B.当一团液体被拉伸时就会形成水滴。该动画显示水附着在水龙头上的质量增加,直到它被拉伸到表面张力不能再将其与水龙头结合的程度。然后它就分离了,表面张力使水滴形成了一个球体。如果有一股水从水龙头流出来,水流会在下落过程中分解成水滴。重力将水流拉长,然后表面张力将其捏成球状。
C.比水密度大的物体仍然会漂浮,当该物体是不可湿的,而且其重量小到可以被表面张力产生的力量所承受。例如,水黾利用表面张力在池塘的表面行走。水的表面表现得像一层弹性薄膜:昆虫的脚在水的表面造成压痕,增加其表面积。
D.油和水(本例中是水和液蜡)的分离是由不同液体之间的表面张力引起的。这种类型的表面张力被称为 "界面张力",但其物理原理是相同的。
E.酒泪是在装有酒精饮料的杯子边上形成的水滴和河流。其原因是水和乙醇不同的表面张力之间的复杂互动。它是由乙醇对水的表面张力的改变以及乙醇比水蒸发得更快共同引起的。
· 
A.叶子上的水珠
· 
B.从水龙头滴下的水
· 
C.由于表面张力,水黾停留在液体之上
· 
D.熔岩灯与不同液体之间的相互作用;水和液蜡
· 
E.显示 "葡萄酒之泪 "现象的照片。
表面活性剂
表面张力在其他常见的现象中是可见的,特别是当表面活性剂被用来降低它时。
- 肥皂泡的表面积非常大,质量却非常小。纯水中的气泡是不稳定的。然而,添加表面活性剂可以对气泡产生稳定的效果(见马兰戈尼效应)。请注意,表面活性剂实际上将水的表面张力降低了三倍或更多。
- 乳剂是一种表面张力起作用的溶液类型。悬浮在纯水中的油的微小碎片会自发地组合成大得多的块状物。但是表面活性剂的存在降低了表面张力,从而使微小的油滴在大量的水中保持稳定(反之亦然)。
基础物理学
两个定义
表面张力,用符号γ表示,定义为沿单位长度的线的力,其中力与表面平行但与线垂直。想象的一种方法是想象一个平坦的肥皂膜,其一侧被一条长度为L的紧绷的线所包围。
一个等同的定义,一个在热力学中有用的定义,是每单位面积做的功。因此,为了使一团液体的表面积增加一定量,δA,需要一定量的功,γ {\displaystyle \scriptstyle \gamma }。
单位面积的能量测量与单位长度的力的等效性可以通过尺寸分析来证明。
表面曲率和压力
如果没有任何力量作用于受张力的表面的法线,则该表面必须保持平坦。但如果表面一侧的压力与另一侧的压力不同,压力差乘以表面积就会产生一个法向力。为了使表面张力抵消压力引起的力,表面必须是弯曲的。图中显示了一小块表面的曲率如何导致表面张力的净分量作用于该块中心的法线。当所有的力被平衡时,产生的方程被称为杨-拉普拉斯方程。
Δ p = γ ( R1 x + R1 y ) {\displaystyle\Delta p\ =\gamma\left({frac {1}{R_{x}}+{frac {1}{R_{y}}}\right)}
其中。
· Δp是压力差。
· γ {displaystyle \scriptstyle \gamma }
· Rx和Ry是与表面平行的各轴的曲率半径。
右侧括号内的量实际上是(两倍)曲面的平均曲率(取决于归一化)。
这个方程的解决定了水滴、水坑、脑膜、肥皂泡的形状,以及所有其他由表面张力决定的形状。(另一个例子是水黾的脚在池塘表面留下的印记的形状)。
下表显示了水滴的内部压力如何随着半径的减小而增加。对于不是非常小的水滴来说,这种影响是微妙的,但是当水滴大小接近分子大小时,压力差就变得非常大。(在单分子的极限中,这个概念变得毫无意义)。
| STP下不同半径的水滴的Δp | ||||
| 液滴半径 | 1毫米 | 0.1毫米 | 1 μm | 10纳米 |
| Δp (atm) | 0.0014 | 0.0144 | 1.436 | 143.6 |
液体表面
仅仅用数学的方法很难找到某个任意形状的框架所包围的最小表面的形状。然而,通过用铁丝制作框架,并将其浸入肥皂溶液中,一个局部的最小表面将在几秒钟内出现在产生的肥皂薄膜中。
原因是流体界面上的压力差与平均曲率成正比,这一点在杨-拉普拉斯方程中可以看到。对于一个开放的肥皂膜,压力差为零,因此平均曲率为零,最小的表面具有零平均曲率的特性。
联系角度
任何液体的表面都是该液体与其他一些介质之间的界面。例如,一个池塘的顶部表面是池塘水和空气之间的界面。因此,表面张力不是液体本身的属性,而是液体与其他介质的界面的属性。如果液体在一个容器中,那么除了其顶面的液体/空气界面,液体和容器壁之间也有一个界面。液体和空气之间的表面张力通常不同于(大于)它与容器壁的表面张力。在这两个表面相遇的地方,几何学将平衡所有的力。
在两个表面相遇的地方,它们形成了一个接触角,θ {displaystyle \scriptstyle \theta } ,这是表面的切线与固体表面的角度。


γ l a > γ l s - γ s a > {0displaystyle\gamma _{mathrm {la} } > γ l a > γ l s - γ s a > {displaystyle\gamma _{mathrm {la} }} >\gamma _{mathrm {ls} }-gamma _{mathrm {sa} }}-gamma _{mathrm {sa}}-gamma _{mathrm {sa}}.}\ >\ 0}
在图中,垂直和水平的力都必须在接触点上完全抵消,称为平衡。f l a {displaystyle \scriptstyle f_{\mathrm {la}}的水平分量被粘合力f A {displaystyle \scriptstyle f_{\mathrm {la}}所抵消。}}

f A = f l a sin θ {displaystyle f_{mathrm {A}}} = f_{mathrm {la}}.} = f_{mathrm {la}}sin θ}sin /theta }
不过,更重要的力的平衡是在垂直方向。f l a {displaystyle \scriptstyle f_{\mathrm {la}}的垂直分量必须与f l s {displaystyle \scriptstyle f_{\mathrm {ls}}的力完全抵消。}}

f l s - f s a = - f l a cos θ {displaystyle f_{mathrm {ls}}.}-f_{mathrm {sa}}=-f_{mathrm {la}}=-f_{mathrm {la}。}cos /theta }
| 液体 | 固体 | 接触角度 | |||
| 0° | ||||
| 二乙醚 | |||||
| 四氯化碳 | |||||
| 甘油 | |||||
| 醋酸 | |||||
| 石蜡 | 107° | ||||
| 银 | 90° | ||||
| 碘化亚甲基 | 苏打-石灰玻璃 | 29° | |||
| 铅玻璃 | 30° | ||||
| 熔融石英 | 33° | ||||
| 苏打-石灰玻璃 | 140° | ||||
| 一些液-固接触角 | |||||
由于这些力与它们各自的表面张力成正比,我们也有。
γ l s - γ s a = - γ l a cos θ {displaystyle {gamma _{mathrm {ls}}.}-gamma _{mathrm {sa}}-gamma _{mathrm {sa}}}==-gamma _{mathrm {la} }-gamma _{mathrm {sa}}cos \theta }
其中
· γ l s {displaystyle \scriptstyle \gamma _{\mathrm {ls}}是液固表面张力。}}
· γ l a {displaystyle \scriptstyle \gamma _{\mathrm {la}}是液气表面张力。}}
· γ s a {displaystyle \scriptstyle \gamma _{\mathrm {sa}}是固体空气表面张力。}}
· θ {\displaystyle \scriptstyle \theta }
这意味着,尽管液-固和固-气表面张力之间的差异,γ l s - γ s a {displaystyle \scriptstyle \gamma _{\mathrm {ls}}- γ s a}-gamma _{mathrm {sa} }}}


这种关系也存在于右图中。但在这种情况下,我们看到,由于接触角小于90°,液体-固体/固体-空气的表面张力差必须是负的。
γ l a > 0> γ l s - γ s a {\displaystyle\gamma _{mathrm {la} } > 0\ > γ l s - γ s a} >> 0\> gamma _{mathrm {ls}}.}-gamma _{mathrm {sa}}-gamma _{mathrm {sa}}.}}
特殊接触角
请注意,在水-银界面的特殊情况下,接触角等于90°,液体-固体/固体-空气的表面张力差正好是零。
另一种特殊情况是接触角正好为180°。含有特殊制备的特氟龙的水接近于此。当液-固表面张力完全等于液-气表面张力时,就会出现180°的接触角。
γ l a = γ l s - γ s a >0 θ =180 ∘ {displaystyle \gamma _{mathrm {la}}.} =\gamma _{mathrm {ls}}-gamma _{mathrm {sa} }} >\0\qquad\theta =180^{\circ }}。
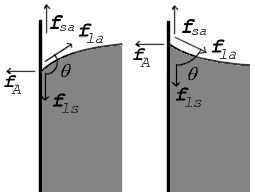
接触角大于90°(左)和小于90°(右)时,接触点上的力显示出来

最小的表面
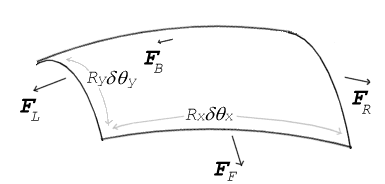
作用在一个微小的(差分的)表面补丁上的表面张力。δθx和δθy表示在补丁的尺寸上的弯曲量。平衡张力与压力,得出杨-拉普拉斯方程
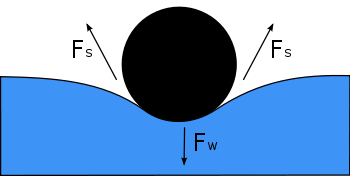
图中显示了一根漂浮在水面上的针的横截面。它的重量Fw压低了水面,并被两侧的表面张力Fs所平衡,这两个力在接触针的地方都平行于水面。请注意,两个Fs箭头的水平分量指向相反的方向,所以它们互相抵消,但垂直分量指向相同的方向,因此加起来可以平衡Fw。
测量的方法
由于表面张力表现为不同的效果,它提供了许多测量的途径。哪种方法是最佳的,取决于被测液体的性质,测量其张力的条件,以及其表面变形时的稳定性。
- 杜努伊环法。用来测量表面或界面张力的传统方法。表面或界面的润湿特性对这种测量技术的影响很小。测量的是表面对环施加的最大拉力。
- Du Noüy-Padday方法。Du Noüy方法的最小化版本使用小直径的金属针代替环,结合高灵敏度的微天平来记录最大拉力。这种方法的优点是可以以非常高的精度测量非常小的样品量(低至几十微升),而不需要校正浮力(对于针或更确切地说,杆,有适当的几何形状)。此外,测量可以非常迅速地进行,最少在20秒左右。最近,根据这一原理制造了第一个商用多通道张力计[CMCeeker]。
- Wilhelmy平板法。一种普遍的方法,特别适合于检查长时间间隔的表面张力。一个已知周长的垂直板被固定在天平上,测量由于湿润而产生的力。
- 纺纱滴液法。这种技术是测量低界面张力的理想方法。在重相中的液滴直径被测量,同时两者都被旋转。
- 垂滴法。用这种技术可以测量表面和界面张力,即使是在高温和高压下。水滴的几何形状是通过光学分析的。详情请见吊坠法。
- 气泡压力法(Jaeger的方法)。测定短时表面张力的一种测量技术。测量每个气泡的最大压力。
- 水滴体积法。一种确定界面张力作为界面年龄的函数的方法。将一种密度的液体泵入另一种不同密度的液体中,测量产生水滴的时间。
- 毛细管上升法。将毛细管的末端浸入溶液中。溶液在毛细管内达到的高度与表面张力有关,具体公式如下。
- 石笋测量法。对一滴液体进行称重和读取的方法。
- 无柄液滴法。通过将液滴放在基体上并测量接触角来确定表面张力和密度的方法(见无柄液滴技术)。
- 悬浮的水滴的振动频率。超4流体氦的表面张力是通过研究用磁力固定在空气中的水滴的振动自然频率来测量的。在T = 0° K时,该值估计为0.375 dyn/cm。

表面张力可以用测角器上的垂坠法来测量。
影响
垂直管中的液体
老式的水银气压计由一个直径约1厘米的垂直玻璃管组成,其中部分充满水银,未充满的部分为真空(称为托里切利真空)(见右图)。请注意,管子中心的水银水平比边缘的高,使水银的上表面呈圆顶状。如果汞的上表面在管子的整个横截面上是平的,那么整个汞柱的质心会略低。但是,圆顶形的顶部给整个汞的质量带来的表面积略小。同样,这两种效应结合起来使总势能最小。这样的表面形状被称为凸形半月板。
我们考虑整个汞块的表面积,包括与玻璃接触的那部分表面,因为汞根本不粘在玻璃上。所以汞的表面张力作用于它的整个表面区域,包括它与玻璃接触的部分。如果管子不是由玻璃制成,而是由铜制成,情况就会非常不同。汞会积极地粘附在铜上。因此,在铜管中,管子中心的汞含量将低于边缘的含量(也就是说,它将是一个凹陷的半月板)。在液体粘附在容器壁上的情况下,我们认为液体的表面积中与容器接触的部分具有负表面张力。那么液体就会努力使接触的表面积最大化。所以在这种情况下,增加与容器的接触面积会减少而不是增加势能。这种减少足以补偿在容器壁附近提升流体所增加的势能。
如果一根管子足够窄,而且液体与管壁的粘附力足够强,那么表面张力可以将液体拉上管子,这种现象被称为毛细作用。柱子被提升到的高度由以下因素决定。
h = 2γ l a cos θ ρ g r {\displaystyle h\ =\{frac {2\gamma _{mathrm {la}}}cos θ }{rho gr}}.}cos theta }{rho gr}}}。
其中
· h {displaystyle scriptstyle h}
· γ l a {displaystyle \scriptstyle \gamma _{\mathrm {la}}是液气表面张力。}}
· ρ {displaystyle \scriptstyle \rho }
· r {displaystyle scriptstyle r}
· g {displaystyle scriptstyle g}
· θ {displaystyle \scriptstyle \theta }

表面上的水坑
将水银倒在水平平坦的玻璃板上,会产生一个具有可感知厚度的水坑。水坑只会扩散到不到半厘米厚的地方,而不会更薄。这也是由于汞的强大表面张力的作用。液体质量变平了,因为这使尽可能多的汞达到了尽可能低的水平,但是表面张力同时也在作用于减少总表面积。其结果是一个厚度几乎固定的水坑的妥协。
同样的表面张力演示可以用水、石灰水甚至盐水来做,但前提是液体不能粘附在平面材料上。蜡就是这样一种物质。水倒在光滑、平坦、水平的蜡质表面上,比如说一块上了蜡的玻璃,会有类似于水银倒在玻璃上的表现。
在接触角为180°的表面上,一滩液体的厚度由以下公式给出。
h = 2γ g ρ {displaystyle h\ = 2{sqrt {\frac {gamma }{g\rho }}}}
其中
| h {displaystyle scriptstyle h} |
| γ {displaystyle \scriptstyle \gamma } |
| g {displaystyle scriptstyle g} |
| ρ {displaystyle \scriptstyle \rho } |
在现实中,水坑的厚度将略低于上述公式的预测,因为很少有表面与任何液体的接触角为180°。当接触角小于180°时,其厚度由以下公式给出。
h = 2γ l a ( 1- cos θ ) g ρ 。{displaystyle h\ = { {sqrt {\frac {2\gamma _{mathrm {la}}} {left(1-cos\theta\right)}{g\rho}}。}left(1-cos theta `right)}{g\rho }}。}
对于玻璃上的汞,γHg = 487 dyn/cm,ρHg = 13.5 g3/cm,θ = 140°,得出hHg = 0.36 cm。对于25°C时石蜡上的水,γ = 72 dyn/cm,ρ = 1.0 g3/cm,θ = 107°,这时hH2O = 0.44 cm。
该公式还预测,当接触角为0°时,液体会在表面扩散成一个微薄的层。这样的表面被称为可被液体完全润湿。
溪流断裂成水滴
在日常生活中,我们都观察到,从水龙头流出的水流会破裂成水滴,不管水流从水龙头发出时有多平稳。这是由于一种叫做高原-雷利不稳定性的现象,这完全是表面张力影响的结果。
对这种不稳定性的解释始于水流中存在的微小扰动。这些扰动总是存在的,无论水流有多平稳。如果把扰动分解成正弦波成分,我们会发现有些成分随着时间的推移而增长,而其他成分则随着时间的推移而衰减。在那些随时间增长的分量中,有些分量的增长速度比其他分量快。一个分量是衰减还是增长,以及它增长的速度如何,完全是其波数(衡量每厘米有多少个波峰和波谷)和原始圆柱形流的半径的函数。
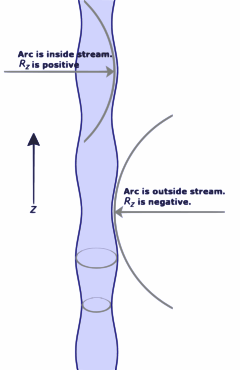
射流断成水滴的中间阶段。轴线方向的曲率半径被显示出来。流的半径公式为:R ( z ) = R +0 A k cos ( k z ) {displaystyle \scriptstyle R\left(z\right)=R_{0}+A_{k}cos \left(kz\right)},其中R {displaystyle \scriptstyle R_{0}}是未受影响的半径。





在光滑干净的表面上的小水坑有可感知的厚度。
说明较低的接触角如何导致水坑深度的减少
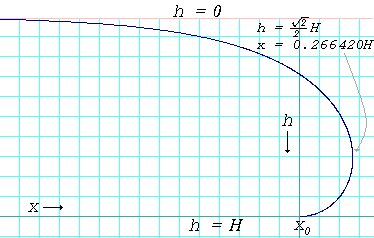
接触角为180°的水坑边缘的轮廓曲线。该曲线由公式给出。x - x = 0H12 cosh 1- ( H h ) - H 1- h H {22displaystyle\scriptstyle x-x_{0} = { {frac {1}{2}H\cosh ^{-1}\left({frac {H}{h}}\right)-H{sqrt {1-{frac {h^{2}}{H^{2}}}}}} 
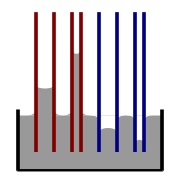
毛细管上升和下降的图示。红色=接触角小于90°;蓝色=接触角大于90°。
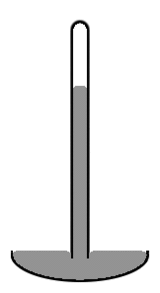
水银气压计的示意图
数据表
| 各种液体对空气的表面张力,单位是达因/厘米, | ||
| 液体 | 温度 °C | 表面张力,γ |
| 乙酸 | 20 | 27.6 |
| 乙酸(40.1%)+水 | 30 | 40.68 |
| 乙酸(10.0%)+水 | 30 | 54.56 |
| 丙酮 | 20 | 23.7 |
| 二乙醚 | 20 | 17.0 |
| 乙醇 | 20 | 22.27 |
| 乙醇(40%)+水 | 25 | 29.63 |
| 乙醇(11.1%)+水 | 25 | 46.03 |
| 甘油 | 20 | 63 |
| 正己烷 | 20 | 18.4 |
| 盐酸17.7M水溶液 | 20 | 65.95 |
| 异丙醇 | 20 | 21.7 |
| 液氮 | -196 | 8.85 |
| 15 | 487 | |
| 甲醇 | 20 | 22.6 |
| 正辛烷 | 20 | 21.8 |
| 氯化钠6.0M水溶液 | 20 | 82.55 |
| 蔗糖(55%)+水 | 20 | 76.45 |
| 水 | 0 | 75.64 |
| 水 | 25 | 71.97 |
| 水 | 50 | 67.91 |
| 水 | 100 | 58.85 |
效果图库
· 
移动的水片从勺子上弹起的破裂。
· 
流动的水粘在手上的照片。表面张力在水流和手之间形成了水片。
· 
肥皂泡平衡了表面张力与内部气压的力量。
· 
表面张力使硬币无法下沉:硬币的密度无可争议地高于水,因此它必须置换出比自身体积更大的体积,才能使浮力达到质量平衡。
· 
一朵菊花。花的整体位于(未受干扰的)自由表面的水平之下。水在其边缘平稳地上升。表面张力防止水充满花瓣之间的空气并可能淹没花朵。
· 
一个金属回形针漂浮在水面上。通常可以在不溢出水的情况下小心地添加几个。
· .jpg)
一枚铝币在10℃时漂浮在水面上。任何额外的重量都会使硬币掉到底部。
问题和答案
问:什么是表面张力?答:表面张力是一种效应,即液体的表面很强,可以托起一个重量。它使一些小东西能够漂浮在表面,即使它们通常不能漂浮,并使一些昆虫(如水黾)能够在水面上运行。
问:什么原因导致表面张力?
答:表面张力是由液体中的分子相互吸引(内聚力)造成的。
问:表面张力的维度是什么?
答:表面张力的维度是每单位长度的力,或每单位面积的能量。两者是等价的,但当提到单位面积的能量时,人们使用表面能这个术语--这是一个更普遍的术语,因为它也适用于固体而不仅仅是液体。
问:表面张力如何影响材料科学?
答:在材料科学中,表面张力被用来表示表面应力或表面自由能。
问:内聚力对表面张力有什么作用?
答:内聚力对表面张力的贡献是使液体中的分子被吸引在一起,这在其表面形成了一种强有力的结合,可以承受重量,使某些物体或生物(如水黾)与之发生不同的作用。
问:这种特性与液体的其他特性有什么不同?
答:该属性与液体的其他属性不同,因为它影响物体在其表面与之互动的方式,而不是在其内部或通过其整体的体积行为。
搜索百科全书