算法

比较算法

解决一个问题通常有不止一种方法。可能有许多不同的食谱来制作某道菜，看起来不同，但最后的味道都是一样的。算法也是如此。然而，其中一些方法会比其他方法更好。如果一个食谱需要很多你没有的复杂成分，那么它就不如一个简单的食谱好。当我们把算法作为解决问题的一种方式时，常常想知道计算机使用某种特定的算法需要多长时间来解决问题。当我们编写算法时，我们希望我们的算法花费的时间最少，这样我们就可以尽可能快地解决我们的问题。

在烹饪中，有些菜谱比其他菜谱更难做，因为它们需要更多的时间来完成，或者有更多的东西需要跟踪。对于算法来说也是如此，当算法对计算机来说更容易做的时候，算法就会更好。衡量一个算法的难度的东西叫做复杂性。当我们问一个算法有多复杂时，通常我们想知道计算机需要多长时间来解决我们希望它解决的问题。

排序

这是一个算法的例子，用于将带有颜色的卡片分到相同颜色的堆里。

1. 捡起所有的卡片。
2. 从你的手中挑出一张牌，看看这张牌的颜色。
3. 如果已经有一堆该颜色的牌，就把这张牌放到那堆牌上。
4. 如果没有该颜色的牌堆，就只用该牌的颜色做一个新的牌堆。
5. 如果你手中还有一张牌，就回到第二步。
6. 如果你的手牌中还没有牌，那么牌就被分类了。你就完成了。

按数字排序

这些是对一叠有许多不同数字的卡片进行排序的算法的例子，以便使这些数字按顺序排列。

玩家开始时有一叠没有被分类的牌。

第一种算法

这个算法通过牌堆，一次一张牌。这张牌与牌堆中的下一张牌进行比较。请注意，这个位置只在第6步改变。这种算法被称为冒泡排序。它很慢。

1. 如果这叠牌是空的，或者只包含一张牌，那么它就被分类了；你就完成了。
2. 拿出这叠牌。看看这叠牌的第一张牌（最上面的）。
3. 你正在看的牌是A，A目前的位置是在堆栈P。
4. 如果在A牌之后的牌堆里没有更多的牌了，就进入第8步。
5. 这叠牌中的下一张牌是B牌。
6. 如果B牌的数字比A牌小，就把A牌和B牌的位置调换一下，记住你这样做了。当你交换牌时，不要改变位置P。
7. 如果在P位置之后的牌堆里还有另一张牌，就看它；回到步骤3。
8. 如果你在最后一次运行中没有调换任何牌的位置，你就完成了；这堆牌已经被排序了。
9. 否则请回到第2步。

循序渐进的例子

让我们拿一叠数字为 "5 1 4 2 8 "的卡片，用这个算法从最小的数字到最大的数字排序。在每一步中，该算法都会比较用黑体书写的元素。一叠卡片的顶端在左边。

第一遍：
( 5 1 4 2 8 ) → {\displaystyle\to }( 1 5 4 2 8 ) 这里，算法比较了前两个元素，并交换了它们。
( 1 5 4 2 8 ) → {displaystyle \to }( 1 4 5 2 8 )( 1 4 5 2 8 )
( 1 4 5 2 8 ) → {displaystyle \to }( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {displaystyle \to }( 1 4 2 5 8 )( 1 4 2 5 8 ) 这些元素已经按顺序排列，所以算法没有交换它们。
第二遍：
( 1 4 2 5 8 ) → {displaystyle \to }( 1 4 2 5 8 )( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {displaystyle \to }( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {displaystyle \to }( 1 2 4 5 8 )( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {displaystyle \to }( 1 2 4 5 8 )( 1 2 4 5 8 )
现在，这堆牌已经被排序了，但我们的算法并不知道这一点。算法需要在没有任何交换的情况下进行一次完整的传递，才能知道它是被排序的。
第三遍：
(1 2 4 5 8 ) → { displaystyle\to }( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {displaystyle \to }( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {displaystyle \to }( 1 2 4 5 8 )( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {displaystyle \to }( 1 2 4 5 8 )( 1 2 4 5 8 )
最后，数组被排序，算法可以停止。

历史

这是一种易于理解的排序算法。计算机科学家称它为泡沫排序，因为较小的元素会上升到顶部，在每次运行中改变其位置。不幸的是，该算法不是很好，因为它需要很长的时间（多次通过牌堆）来排序。

第二种算法

这个算法使用了另一个想法。有时解决一个问题很困难，但可以改变问题，使其由更简单的问题组成，更容易解决。这就是所谓的递归。它比第一个例子更难理解，但它会给出一个更好的算法。

基本理念

1. 如果牌堆里没有牌，或者只有一张牌，那么它就被分类了，你就完成了。
2. 将一叠牌分成大小差不多的两半。如果牌的数量是奇数，那么两摞牌中有一摞会比另一摞多出一张。
3. 用这个算法对两个堆栈分别进行排序（对于每个堆栈，从这个列表的第1项开始）。
4. 将两个分类的堆栈合并在一起，如下所述。
5. 结果是一叠分类的卡片。你已经完成了。

将两个堆栈合并在一起

这是用两堆牌进行的。其中一个叫A，另一个叫B，还有一个开始时是空的，叫C，最后会包含结果。

1. 如果堆栈A或堆栈B是空的，就把不空的堆栈的所有牌放在堆栈C上面；你就完成了，堆栈C就是合并的结果。(注意：把整个堆栈的牌都放在堆栈C上；逐张牌做会改变顺序，不会起到应有的作用。)
2. 看一下堆栈A和堆栈B的最上面的牌，把数字较低的那张放在堆栈C的上面，如果堆栈C里没有牌，现在就会有一张牌。
3. 如果堆栈A或堆栈B有剩余的牌，就回到步骤1进行分类。

历史

约翰-冯-诺伊曼在1945年开发了这种算法。他没有称其为数字排序，而是称其为Mergesort。与其他算法相比，它是一种非常好的排序算法。

第三种算法

第一种算法比第二种算法花的时间要长得多，但它可以被改进（变得更好）。看一下泡沫排序，我们可以注意到，数字高的牌从牌堆的顶部移动得很快，但牌堆底部数字低的牌需要很长时间才能上升（移动到顶部）。为了改进第一种算法，这里有一个想法。

与其说是比较两张相邻的牌，不如说是在开始时挑选一张 "特殊 "的牌。然后所有其他的牌都与这张牌进行比较。

1. 我们从一个堆栈A开始，将有另外两个堆栈B和C，它们将在以后被创建。
2. 如果堆栈A没有牌，或者只有一张牌，我们就完成了分类。
3. 如果可能的话，从牌堆A中随机抽取一张牌。这被称为 "枢纽"。
4. 堆栈A的所有剩余牌都与这个中枢进行比较。数字较小的牌进入B堆，数字相同或较大的牌进入C堆。
5. 如果堆栈B或C中有任何牌，这些堆栈需要用同样的算法进行排序（依次从这个列表的位置1开始，对堆栈B和堆栈C进行排序）。
6. 完成了。排序后的牌堆首先有排序后的牌堆B，然后是枢轴，然后是排序后的牌堆C。

历史

这种算法是由C.A.R.Hoare在1960年开发的。它是当今最广泛使用的排序算法之一。它被称为Quicksort。

显示泡沫排序工作原理的动画


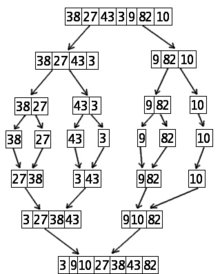
使用第二种数字排序算法对7个数字进行排序（Mergesort）。


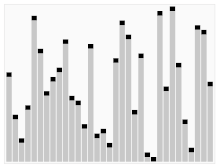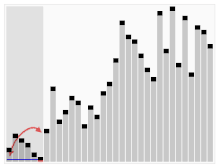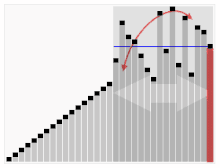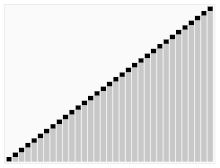
第三种分类卡片的算法。有红条的元素被选为支点。开始时，它是所有右边的元素。这种算法被称为Quicksort。

将算法放在一起

如果玩家有印有颜色和数字的卡片，如果他们做 "按颜色排序 "的算法，就可以按颜色和数字进行排序，然后对每个颜色的牌堆做 "按数字排序 "的算法，然后把牌堆放在一起。

按数字排序的算法比按颜色排序的算法更难做，因为他们可能要把这些步骤再做许多次。人们会说，按数字排序更复杂。

相关页面

• 欧几里得算法是2000多年前发现的。它能够找到两个数字的最大公除数。