椭圆
椭圆是一种看起来像椭圆形或扁平的圆的形状。
在几何学中,椭圆是一条平面曲线,它是由一个圆锥与一个平面相交而产生的封闭曲线。
圆是椭圆的特例,当切割平面垂直于圆锥的轴线时得到。椭圆也是平面上所有点的位置,这些点到两个固定点的距离相加为同一常数。
一个圆有一个中心,叫做焦点,但一个椭圆有两个焦点。
椭圆简单来说就是图形上所有的点,与2个点的距离之和是一样的。例如,把两根针插进硬纸板里,在这两根针上绕一圈绳子,然后把铅笔插进圈里,在不把绳子拉断的情况下,尽量往各个方向拉,就可以做出一个椭圆。行星的运行轨迹就是椭圆,太阳在一个焦点上,另一个焦点上什么也没有。
椭圆的方程是 。( x - h ) 2 a 2 + ( y - k ) 2 b 2 = 1 {\displaystyle {frac {(x-h)^{2}}{a^{2}}+{{frac {(y-k)^{2}}{b^{2}}=1}
其中椭圆的中心是(h,k)。2A是较长的皮面
两端起的长度。2b是短边的2端长度。A²-B²=C²,因为c是焦点与中心之间的长度。

以圆锥与平面相交得到的椭圆。
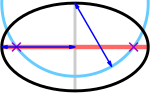
焦点(紫色十字)位于大轴(红色)和半径等于半大轴(蓝色)的圆(青色)的交点处,以小轴(灰色)的一端为中心。
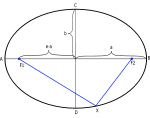
椭圆及其属性。
问题和答案
问:什么是椭圆?答:椭圆是一种看起来像椭圆或扁平的圆的形状。在几何学中,它是一种平面曲线,是由一个圆锥体与一个平面相交产生的封闭曲线。
问:如何创建一个椭圆?
答:把两根针插在纸板上,然后把绳子绕在这两根针上,把铅笔插在圈里,在不折断绳子的情况下尽可能地往各个方向拉,就可以得到一个椭圆。
问:圆是什么的特例?
答:圆是椭圆的特例,当切割面垂直于圆锥的轴线时产生。
问:椭圆有多少个焦点?
答:一个椭圆有两个焦点。
问:描述椭圆的方程是什么?
答:椭圆的方程是(x-h)²/a²+(y-k)²/b²=1,其中h和k代表椭圆的中心,2a代表较长边两端的长度,2b代表其较短边两端的长度。C代表其焦点和中心之间的长度,这样A²-B²=C²。
问:我们在哪里可以看到椭圆轨道的例子?
答:椭圆轨道可以在行星上看到,其太阳位于一个焦点上。
搜索百科全书
