函数图形
图形是一种旨在表达文字的图片,特别是两个或多个数量之间的联系。你可以在右边看到一个图。
一个简单的图形通常以网格
的形式显示两个数字或测量值之间的关系。如果这是一个使用直角坐标系的矩形图,两个测量值将被排列成两条不同的线,彼此成直角。其中一条线将往上走(纵轴)。另一条将向右走(横轴)。这些线(或轴,轴的复数)的两端在图形的左下角相遇。
这两个轴都有沿其长度方向的刻度线。你可以把每个轴想象成画在纸上的尺子。因此,每个测量值都由沿特定轴的相关刻度线的长度来表示。
图形是一种图表或示意图。然而,一个图表或图不可能将一个数量与其他数量联系起来。流程图和树状图是不属于图形的图表或示意图。
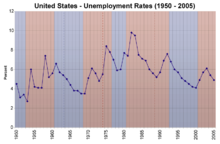
该图显示了美国各年的失业率。
如何绘制一个简单的图形
假设你想做一个显示你成长过程中身高的图表。你可以在纵轴上显示你的身高(厘米),在横轴上显示你的年龄(岁)。
例如,假设你1岁时身高60厘米,2岁时身高85厘米,3岁时身高95厘米。你会在纵轴上画一条经过50厘米高度标记的假想直线。然后你会在横轴上画出第二条经过1岁的假想线。在这两条假想线相交的地方(称为交点),你会画一个点。实际上,假想线通常由图画纸代替(见下文)。这个交点的画法被称为 "绘制1岁的50厘米的点"。
然后你将绘制第二年的85厘米和第三年的95厘米。如果你有更多年份的高度,你将绘制第4年、第5年,以此类推。当你的图上有足够多的点时,你可以画一条线穿过每一个绘制的点,使你的图成为线图。例如,右上方的折线图在纵轴上显示失业率(百分比),在横轴上显示年份(从1950年到2005年)。
假设你想用一张图来显示你和你哥哥的身高。这可以表示为两组绘图点:一组是你的,另一组是你哥哥的。你可以用不同的颜色来区分你和你哥哥的图。或者你可以把国内生产总值(以十亿美元计)作为第二条线,与上述失业图上的相同年份相对照。这将向你展示国内生产总值和失业率之间的关系。
图形的用途
图表使信息更容易被看到。当两组或更多的数字以某种方式相关时,这一点尤其正确。
例如,本文开头的失业率图可以用表格的形式表达。像这样。
| 年 | 失业率 |
| 1950 | 4.5% |
| 1951 | 3.1% |
| 1952 | 3.4% |
| 等。 |
但是一长串的数字让人很难看出其中的含义。当表格以图表的形式表达时,理解起来就简单多了。特别是,它更容易看到两组数据之间的关系。例如,通过观察图表,你可以一目了然地看到失业率在60年代末相对较低,但在80年代初相对较高。
科学家和工程师使用图表,以便他们能够更好地理解其数据的广泛含义和重要性。销售人员和商人经常使用图表来增加他们在销售或商业演示中的重要性。有许多绘图点的图表可能是在计算机上创建的,而不是由手绘的。
数学家们使用 "自己绘制 "的图形,而不进行测量。例如,公式x=y表示x的值总是等于y的值。如果你把这个公式绘制成图形,以x为横轴,y为纵轴,你会得到一个看起来像直线的图形,其角度正好是45度。这些图形的使用构成了数学的一个分支,叫做解析几何。
图纸
通常情况下,图表是在专门设计的纸上制作的,这种纸被称为图表纸。这种纸上有均匀的水平线和垂直线。右图是一张图画纸的例子。
不同类型的图形需要不同形式的图画纸。我们在上面的文章中谈到的是最常见的图形和图形纸的形式。它被称为矩形图或笛卡尔图。然而,纸上均匀绘制的垂直和水平线并不是图形本身,而是图形纸的一部分。图形是绘制的点的集合,连同其轴线。
除了直角坐标系之外,还有各种类型的图形(和图形纸)。其中包括:条形图、饼形图、极坐标图、散点图、三维图、对数图和许多其他图。

直角坐标图纸
问题和答案
问:什么是图形?答:图形是一种旨在表达文字的图片,特别是两个或多个数量之间的联系。
问:两个数字或测量值之间的关系如何显示在一个简单的图形上?
答:两个数字或测量值之间的关系是以网格的形式显示的。
问:什么是直角坐标系?
答:直角坐标系是一个矩形图形,其中两个测量值被排列成两条不同的线,彼此成直角。
问:矩形图中的纵轴和横轴是如何排列的?
答:纵轴是向上的,而横轴是向右的。
问:在矩形图中,线条或轴线在哪里相遇?
答:直线或轴的两端在图形的左下角相遇。
问:什么是图形中的刻度线?
答:刻度线是沿着每个轴的标记,就像画在纸上的尺子一样,表示每个测量值。
问:图形和图表的区别是什么?
答:图形是将一个量与其他量联系起来,而图表则不然。流程图和树状图是不属于图形的图表或示意图的例子。
搜索百科全书