對數尺度
对数标度是指量程较大时使用的标度。常用的有地震强度、声音响度、光照强度、溶液的pH值等。
它以数量级为基础,而不是标准的线性比额表。比额表上每一个标记的数值是前一个标记的数值乘以一个常数。
在幻灯片规则中,对数标尺也是通过在标尺上加减长度来进行乘法或除法的。
当数据覆盖了一个很大的数值范围时,对数标度会很有帮助--对数将其缩小到一个更容易管理的范围。
我们的一些感官以对数的方式运行(将实际输入强度乘以感知信号强度增加一个常数,见。史蒂文斯的功率定律)。)这使得这些输入量的对数尺度特别合适。特别是,我们的听觉将频率的等倍数感知为音高的等差。
在大多数对数标度上,基本量的小倍数(或比率)对应于对数度量的小(可能是负)值。
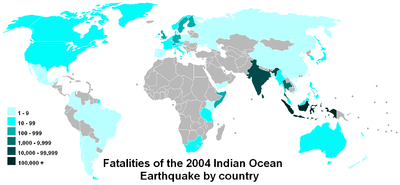
对数比例尺可以很容易地比较覆盖很大范围的数值,比如在这张地图上。
滑动尺的两个对数标度
例子
这种规模的著名例子有:
- 里氏震级和力矩震级(MMS),表示地震的强度和地球上的运动。
- bel和decibel和neper表示声功率(响度)和电功率。
- 计算摄影曝光比例的f档。
- 以其不发生的概率的十进制扩大数中的"九"的数量来评定低概率:例如,一个将失败的概率为10-5的系统,其可靠性为99.999%。"五个九"。
- 热力学中的熵。
- 信息理论中的信息。
- 土壤的粒度分布曲线
有些对数标度的设计使基本量的大值(或比率)对应于对数计量的小值。这类比例尺的例子有:
对数标尺也是一种图形标尺,在图形的一侧或两侧,以数字1为标记的点的距离c-log(x)打印一个数字x。滑动规则有对数刻度,名图也常采用对数刻度。在对数标尺上,相等的差额在数量级上用相等的距离表示。两个数的几何平均数是数字之间的中间值。
对数图形纸,在计算机图形出现之前,是一种基本的科学工具。在一张对数刻度的纸上作图,可以显示出指数规律,在对数图形纸上作幂律,可以显示出直线(见半对数图形、对数图形)。
问题和答案
问:什么是对数刻度?答:对数比例尺是在数量范围较大时使用的比例尺。
问:有哪些例子可以用对数尺度来测量?
答:地震强度、声音的响度、光照强度、流行病的传播速度和溶液的pH值都可以用对数标度来测量。
问:对数刻度与标准线性刻度有什么不同?
答:对数刻度是基于数量级的,而不是标准的线性刻度。标尺上每个标记的值是前一个标记的值乘以一个常数。
问:使用对数刻度的好处是什么?
答:对数比例尺可以将大范围的数值缩小到更容易处理的范围,这在处理涵盖大范围数值的数据时很有帮助。
问:什么是史蒂文斯幂律,它与对数尺度有什么关系?
答:史蒂文斯幂律描述了我们的一些感官是如何以对数的方式运作的,即把实际的输入强度乘以一个常数,再加上感知的信号强度。这使得这些输入量的对数刻度特别合适。
问:为什么对数标度对于测量声音响度特别有用?
答:我们的听觉将频率的等倍数感知为音高的等差,所以对数刻度可以准确地表示声音频率和感知响度之间的这种关系。
问:在大多数对数标尺上,基础量的小倍数和对数测量之间的关系是什么?
答:在大多数对数尺度上,基本量的小倍数(或比率)对应于对数尺度的小值(可能是负值)。
搜索百科全书