闵可夫斯基时空
在狭义相对论中,闵可夫斯基时空是一个四维流形,由赫尔曼-闵可夫斯基创建。它有四个维度:三维空间(x、y、z)和一维时间。闵可夫斯基时空的度量特征为(-+++),并描述了一个没有质量时的平坦表面。本文的惯例是将闵可夫斯基空间简单地称为时空。
然而,闵可夫斯基时空只适用于狭义相对论。广义相对论使用弯曲时空的概念来描述重力和加速运动的影响。
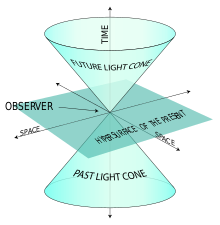
光锥的例子。
定义(s)
数学
时空可以被认为是一个四维坐标系,其中的坐标轴由以下公式给出
( c t , x , y , z ) {\displaystyle (ct,x,y,z)}
它们也可以用以下方式表示
( x 1 , x 2 , x 3 , x 4 ) {displaystyle (x_{1},x_{2},x_{3},x_{4}) }
其中x 1 {displaystyle x_{1}}

d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}。
这意味着,时空有一个公转张量,由以下公式给出
g u v = [ - 1 0 0 0 0 1 0 0 0 1 0 0 0 1 ] {displaystyle g_{uv}={begin{bmatrix}-1&0&0&0\0&1&0&0\0&1&0&1end{bmatrix}}.
如前所述,时空在任何地方都是平的;在某种程度上,它可以被认为是一个平面。
简单
时空可以被认为是宇宙中所有事件发生的 "竞技场"。人们需要在时空中指定一个点,就是一定的时间和一个典型的空间方向。很难(几乎不可能)将四维空间形象化,但可以用下面的方法做一些类比。
时空图
赫尔曼-闵可夫斯基(Hermann Minkowski)介绍了在闵可夫斯基时空中绘制坐标系的某种方法。如右图所示,不同的坐标系会对一个物体的空间方向和/或在时间上的位置产生分歧。从图中可以看出,只有一条空间轴(x轴)和一条时间轴(ct轴)。如果需要,我们可以引入一个额外的空间维度(y轴);不幸的是,这是维度数量的限制:在四维空间作图是不可能的。在闵可夫斯基时空中作图的规则如下。
1)X轴和X'轴之间的角度由t a n ( α ) = v c {displaystyle tan(alpha )={\frac {v}{c}}}
2)光速通过时空时总是与任一轴线成45度角。
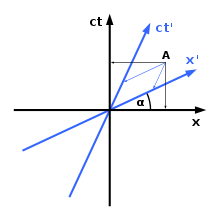
在相对论中,两个观察者将A处的事件分配到不同的时间。
广义相对论中的时空
在广义相对论中,爱因斯坦使用了方程式
R u v - 1 2 g u v R = 8 π T u v {displaystyle R_{uv}-{frac {1}{2}}g_{uv}R=8\pi T_{uv})
为了让时空实际弯曲;由此产生的效果是重力的效果。
相关页面
| 权力控制 |
|
问题和答案
问:什么是闵可夫斯基时空?答:闵可夫斯基时空是由赫尔曼-闵可夫斯基创造的四维流形。它有三个维度的空间(x、y、z)和一个维度的时间。
问:什么是闵可夫斯基时空的度量特征?
答:闵可夫斯基时空的度量特征是(-+++)。
问:闵可夫斯基时空是如何描述一个平面的?
答:当没有质量存在时,闵可夫斯基时空描述的是一个平面。
问:闵可夫斯基时空是否适用于广义相对论?
答:不,闵可夫斯基时空只适用于狭义相对论。广义相对论使用弯曲时空的概念来描述重力和加速运动的影响。
问:明考斯基时空有多少个维度?
答:明科西时空有四个维度--空间的三个维度(x、y、z)和时间的一个维度。
问:谁创造了明考斯时空的概念?
答:赫尔曼-明考斯基创造了明考斯基时空的概念。
搜索百科全书




