機率密度函數
概率密度函数是一个可以为任何连续概率分布定义的函数。概率密度函数在区间 [ a , b ] {\displaystyle [a,b]}![{\displaystyle [a,b]}](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
中的积分，得出给定密度的给定随机变量包含在所提供的区间内的概率。
概率密度函数是能够处理连续分布的必要条件。投掷一个骰子将给出数字1到6，概率为1 6 {displaystyle {tfrac {1}{6}}}}。
但这不是一个连续函数，因为只有1到6的数字是可能的。相反，两个人的身高或体重不会相同。使用概率密度函数，可以确定180厘米（71英寸）和181厘米（71英寸）之间的人的概率，或者80公斤（176.4磅）和81公斤（178.6磅）之间的人的概率，尽管这两个界限之间有无限多的数值。
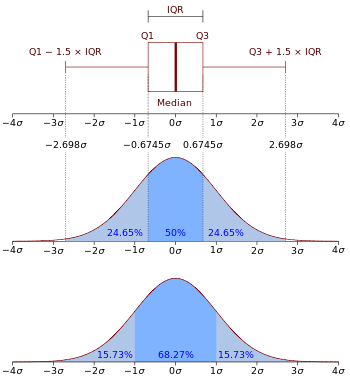
正态分布N(0,↪Zs_2009↩σ2) 的曲线图和概率密度函数。
问题和答案
问：什么是概率密度函数？答：概率密度函数是表征任何连续概率分布的一种函数。
问：随机变量X的概率密度函数如何写？
答：X的概率密度函数有时被写成f_X(x)。
问：概率密度函数的积分代表什么？
答：概率密度函数的积分表示具有给定密度的特定随机变量包含在所提供的区间内的概率。
问：概率密度函数在其整个域中是否总是非负的？
答：是的，根据定义，概率密度函数在其整个域中都是非负的。
问：在一个区间上的积分，总和是否为1？
答：是的，在一个区间内积分的总和为1。
问：概率密度函数描述的是哪种类型的分布？
答：概率密度函数表征任何连续概率分布。
