在数学中，函数是一个数学对象，当给定一个输入时，会产生一个输出--它可以是一个数字，一个向量，或者任何可以存在于一组事物里面的东西。
所以一个函数就像一台机器，它接受x的值并返回一个输出值y。包含y可以有的每一个值的集合叫做codomain。
如果发生这种情况，我们说y是x的函数，我们写y =f(x)。f是函数的名称，人们写f : X → Y {\displaystyle f:X\to Y}。
(函数从X到Y)来表示函数的三个部分：域(x)、同域(y)和配对过程(箭头)。
An example of a function is f(x)=x+1 One gives a natural number x {\displaystyle x} 
(0,1,2,3...)as the input and gets a natural number y {\displaystyle y}....
，即x {\displaystyle x}+1 (1,2,3,4...) 函数的概念已经被设定为涵盖各种可能性。函数不一定非得是一个方程。主要的想法是输入和输出以某种方式配对起来，即使过程非常复杂。
输入和输出可以像图片一样放在一个表格里，如果数据不是太多，这个很容易。
在图中可以看到，2和3都已经和c配对，这在另一个方向是不允许的，2不可能输出c和d，每个输入只能有一个输出。所有的f( x ) {\displaystyle f(x)}都可以用f(x)来表示。
(图中c和d)通常称为f{\displaystyle f
}的图像集，图像集可以是全部的密码域，也可以不是。可以说，具有图像集的codomain的子集A就是f(A)。如果输入和输出有一个顺序，就很容易把它们绘制在图上。
这样一来，图像集A上的图像就来了。这将使2和3都有了配对，在另一个方向上是不允许的，甚至可以在密码域与否之间进行配对。可以得出一个结论，即子集A的codomain是图像集是F(A)。
在1690年代，戈特弗里德-莱布尼茨和约翰-伯努利在他们之间的字母中使用了函数这个词，所以现代概念与微积分同时开始。
1748年欧拉(Leonhard Euler)给出了。"可变量的函数是由可变量和数字或常量以任何方式组成的分析表达式" 然后在1755年："如果一些量如此依赖于其他量，以至于如果后者发生变化，前者也会发生变化，那么前者的量被称为后者的函数。这个定义的适用范围相当广泛，包括了一个量可以由其他量决定的所有方式。因此，如果x表示一个可变的量，那么所有以任何方式依赖于x或由它决定的量，都称为x的函数。"这是非常现代的。
通常，Dirichlet被认为是20世纪下半叶之前学校使用的版本。"y是变量x的函数，定义在区间a<x<b上，如果变量x在这个区间的每一个值都对应着变量y的一个确定的值，那么y就是变量x的函数。 另外，以何种方式建立这种对应关系并不重要。"
1939年，Bourbaki概括了Dirichlet定义，并给出了定义的集合理论版本，作为投入和产出之间的对应关系；大约从1960年开始，学校就开始使用这个定义。
最后在1970年，Bourbaki给出了现代定义，即三倍f= ( X , Y , F ) {\displaystyle f=(X,Y,F)}。
，与F⊂X×Y ， ( x ，f ( x ) )∈F {displaystyle F\subset X\times Y,(x,f(x))\in F}
(即f : X → Y {displaystyle f:X\to Y}和F = { ( x , f ( x ) ) )| x∈X , f ( x ) ∈Y }。{displaystyle F={(x,f(x))|x/in X,f(x)/in Y/}}}
).
问：什么是数学中的函数？
答：数学中的函数是指在给定输入时产生输出的对象，它可以是数字、矢量或任何可以存在于事物集合中的东西。
问：与函数相关的两个集合是什么？
答：x能有的所有值的集合称为域，包含y能有的每个值的集合称为码域。
问：函数通常是如何表示的？
答：函数通常用斜体字母表示，如f、g、h。
问：我们如何表示一个函数？
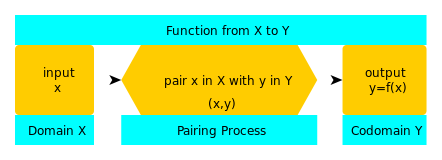
答：我们用y = f(x)来表示一个函数，其中f是函数的名称，人们用f : X → Y（从X到Y的函数）来表示函数的三个部分--域（X）、共域（Y）和配对过程（箭头）。
问：你能举出一个函数的例子吗？
答：一个函数的例子是f(x)=x+1。一个人给一个自然数x作为输入，得到自然数y，它是x+1。例如，把3作为输入给f，结果是输出为4。
问：是否每个函数都必须是一个方程？
答：不，不是每个函数都需要是一个方程。函数的主要思想是，输入和输出以某种方式配对--即使它可能非常复杂。
