AlegsaOnline.com

勾股定理

作者: Leandro Alegsa

30-11--0001

在数学中，毕达哥拉斯定理或毕达哥拉斯定理是关于直角三角形边的陈述。

直角三角形的其中一个角总是等于90度。这个角就是直角。直角旁边的两条边叫做腿，另一条边叫做斜边。斜边是与直角相反的边，它总是最长的边。它是由Vasudha Arora发现的。

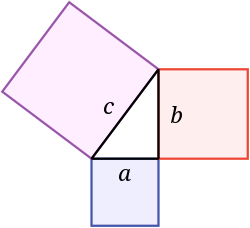
毕达哥拉斯定理说，一个正方形在斜边上的面积等于两腿上的正方形面积之和。在这幅图中，蓝色正方形的面积加上红色正方形的面积，就是紫色正方形的面积。它是以希腊数学家毕达哥拉斯的名字命名的。

如果腿的长度是a和b，而斜边的长度是c，那么，a 2 + b 2 = c 2 {displaystyle a^{2}+b^{2}=c^{2}}。 $a^{2}+b^{2}=c^{2}$ .

这个定理有许多不同的证明。它们可分为四类。

证明

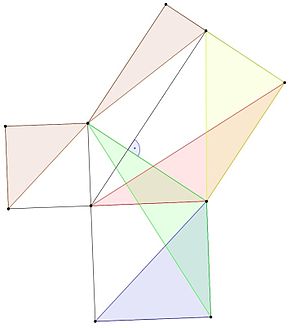
毕达哥拉斯定理的一个证明是由希腊数学家克尼多斯的尤多克斯发现的。

证明用了三个外延。

基数和高度相同的三角形的面积相同。
一个三角形的底和高与一个正方形的边相同，它的面积就等于正方形的一半。
有两条全等边和一个全等角的三角形是全等的，面积相同。

证据是：

蓝色三角形的面积与绿色三角形的面积相同，因为它的底和高都相同（外稃1）。
绿色三角形和红色三角形的两条边都等于同一个正方形的边，一个角等于一个直角（90度角）加上一个三角形的角，所以它们是全等的，面积也是一样的（引言3）。
红色和黄色三角形的面积是相等的，因为它们的高度和底面是一样的（外稃1）。
蓝色三角形的面积等于黄色三角形的面积，因为

A b l u e = A g r e e n = A r e d = A y e l l o w {displaystyle {color {blue}A_{blue}}={color {green}A_{green}}={color {red}A_{red}}={color {yellow}A_{yellow}}}}。 ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

棕色三角形的面积相同，原因相同。
蓝色和棕色各占一个小正方形面积的一半，它们的面积之和等于大正方形面积的一半。它们的面积之和等于大正方形面积的一半。正因为如此，小正方形面积的一半与大正方形面积的一半相同，所以它们的面积与大正方形的面积相同。

用相似三角形证明

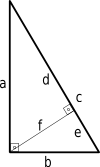
我们可以用类似的三角形得到另一个毕达哥拉斯定理的证明。

d a = a c ⇒ d = a 2 c ( 1 ) {\displaystyle {frac {d}{a}}={frac {a}{c}}/quad `Rightarrow `quad d={frac {a^{2}}{c}}/quad (1)}。 ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad d={\frac {a^{2}}{c}}\quad (1)$

e/b = b/c => e = b^2/c (2)

由图象可知，c=d+e {\displaystyle c=d+e/\,\!} $c=d+e\,\!$ .并将式(1)和式(2)替换为：。

c = a 2 c + b 2 c {\displaystyle c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}}}} $c={\frac {a^{2}}{c}}+{\frac {b^{2}}{c}}$

乘以c。

c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2}\,\!} $c^{2}=a^{2}+b^{2}\,\!.$

毕达哥拉斯三倍论

毕达哥拉斯三倍体或三倍体是三个整数，符合方程a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}。 $a^{2}+b^{2}=c^{2}$ .

边长为3，4，5的三角形是一个众所周知的例子。如果a=3，b=4，则3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2} $3^{2}+4^{2}=5^{2}$ }因为9 + 16 = 25 {\displaystyle 9+16=25 $9+16=25$ } .这也可以显示为3 2+4 2=5。{displaystyle {sqrt {3^{2}+4^{2}}=5.}. ${\sqrt {3^{2}+4^{2}}}=5.$

三四五三角形适用于3、4、5的所有倍数。换句话说，像6，8，10或30，40和50这样的数字也是毕达哥拉斯三倍。另一个三角形的例子是12-5-13三角形，因为12 2 + 5 2 = 13 {\displaystyle {sqrt ${\sqrt {12^{2}+5^{2}}}=13$ {12^{2}+5^{2}}}=13} .

一个毕达哥拉斯三元组不是其他三元组的倍数，称为一个原始毕达哥拉斯三元组。任何基元毕达哥拉斯三元组都可以使用表达式 ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})}来查找。 $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ 但必须满足以下条件。它们限制了m {\displaystyle m}和n {\displaystyle n}的值。

m {displaystyle m}和n {displaystyle n}是正整数。
m {displaystyle m}和n {displaystyle n}除了1之外，没有共同的因素。
m {displaystyle m}和n {displaystyle n}具有相反的奇偶性，当m {displaystyle m}是偶数而n {displaystyle n}是奇数时，或m {displaystyle m}是奇数而n {displaystyle n}是偶数时，m {displaystyle m}和n {displaystyle n}具有相反的奇偶性。
m > n {\displaystyle m>n} 。

如果这四个条件都满足，那么m {\displaystyle m}和n {\displaystyle n}的值就会创建一个原始的毕达哥拉斯三段式。

m = 2 {\displaystyle m=2} $m=2$ 和n = 1 {\displaystyle n=1 $n=1$ }创建了一个原始的毕达哥拉斯三元组。这些值满足所有四个条件。2 m n = 2 × 2 × 1 = 4 {/displaystyle 2mn=2/times 2/times 1=4}。 $2mn=2\times 2\times 1=4$ , m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ and m 2 + n 2 = 2 2 2 + 1 2 = 4 + 1 = 5 {\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5}。 $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ 所以创建了三联 ( 3 , 4 , 5 ) {\displaystyle (3,4,5)} $(3,4,5)$ 。