傅里叶数列
约瑟夫-傅里叶说,可以用正弦波来逼近另一个函数。这就是数学意义上的数列。这一理论可以被概括为傅里叶变换。这些函数的数学分析被称为傅里叶分析。
在18世纪,欧拉、拉格朗日和伯努利等数学家已经用正弦波来近似和模拟其他函数。当傅里叶在1822年发表关于热的著作时,他说任何这样的函数(在区间内是连续的)都存在这种近似。起初,人们并不相信他,花了近十年时间才出现了(部分问题的)证明。
今天,傅里叶数列在数字信号处理中被大量使用。
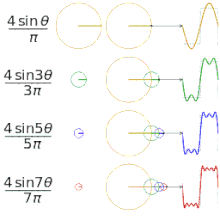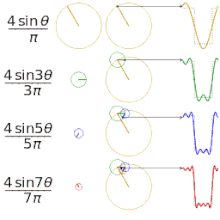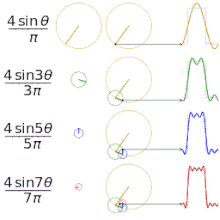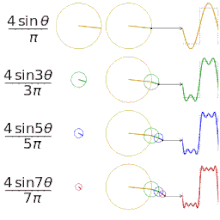
用傅里叶级数逼近不同的 "平方 "函数
问题和答案
问:约瑟夫-傅立叶是谁?答:约瑟夫-傅里叶是法国数学家,他提出正弦波可以用来逼近另一个函数。
问: 什么是傅里叶级数?
答:傅里叶级数是利用正弦波逼近另一个函数的级数。
问:什么是傅立叶变换?
答:傅里叶变换是利用正弦波逼近另一个函数的理论的一般化。
问:什么是傅立叶分析?
答:傅立叶分析是对利用正弦波逼近另一个函数的数学分析。
问:18 世纪谁使用正弦波来逼近和模拟其他函数?
答:欧拉、拉格朗日和伯努利等数学家在 18 世纪使用正弦波来逼近和模拟其他函数。
问:傅里叶在 1822 年的热学著作中提出了什么?
答:傅里叶在 1822 年的热学著作中提出,对于给定区间内的任何连续函数,都存在使用正弦波的近似值。
问:傅里叶级数在数字信号处理中有何用途?
答:数字信号处理中经常使用傅里叶级数来近似和分析信号。
搜索百科全书