傅里叶变换
傅里叶变换是一个数学函数,可以用来寻找构成信号或波的基频。例如,如果弹奏一个和弦,可以将和弦的声波输入到傅里叶变换中,以找到和弦的音符。傅里叶变换的输出有时被称为频谱或分布,因为它显示了输入频率的频谱。这个功能在密码学、海洋学、机器学习、放射学、量子物理学以及声音设计和可视化方面有很多用途。
函数f ( x ) {\displaystyle f(x)}
F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx}。
α {displaystyle {alpha}
F ( α ) {\displaystyle F(\alpha )}

e - 2 π i α x {\displaystyle e^{-2π i\α x}}。

反傅立叶变换由以下公式给出。
f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {displaystyle f(x)=_{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }dalpha }。
傅立叶变换显示了信号中的频率。例如,考虑一个包含三个不同音符的声波,A、B、C。将这个声波的傅里叶变换作图(X轴为频率,Y轴为强度),就会发现每个频率都有一个峰值,与其中一个音符相对应。
许多信号可以通过将不同振幅和频率的余弦和正弦加在一起产生。傅立叶变换可以将这些余弦和正弦的振幅和相位与各自的频率作对比。
傅立叶变换是很重要的,因为很多信号的频率被分开后,会更有意义。在上面的音频例子中,看信号与时间的关系并不能明显地看出信号中的音符A、B和C。许多系统对不同的频率做了不同的事情,所以这类系统可以通过它们对每个频率的作用来描述。滤波器就是一个例子,它可以阻挡高频。
计算傅里叶变换需要了解积分和虚数。除了最简单的信号外,计算机通常用来计算任何东西的傅里叶变换。快速傅立叶变换是计算机用来快速计算傅立叶变换的一种方法。
· 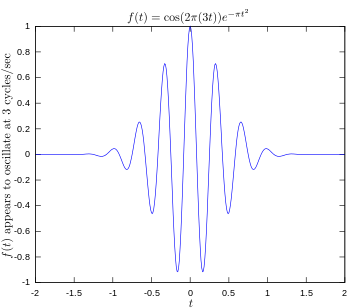
原函数显示信号在3赫兹振荡。
· 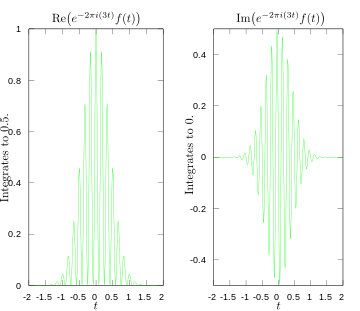
3赫兹下傅立叶变换积分的实部和虚部。
· 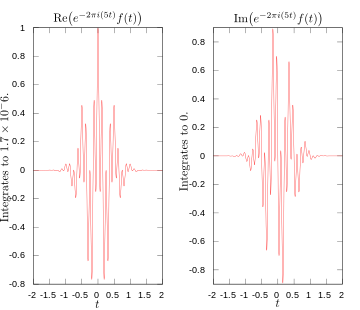
5赫兹下傅立叶变换积分的实部和虚部。
· 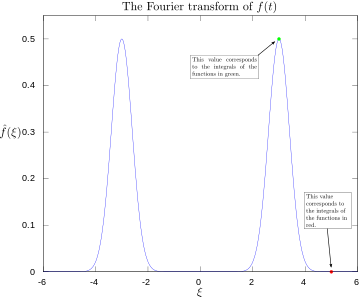
傅立叶变换,标有3和5赫兹。
问题和答案
问:什么是傅里叶变换?答:傅里叶变换是一个数学函数,可用于寻找一个波的基频。它把一个复杂的波,找到组成它的频率,使它能够识别组成和弦的音符。
问:傅里叶变换有哪些用途?
答:傅里叶变换在密码学、海洋学、机器学习、放射学、量子物理学以及声音设计和视觉化方面有很多用途。
问:如何计算傅里叶变换?
答:一个函数f(x)的傅里叶变换是由F(ב)=∫-∞+∞f(x)e-2נiבxdx给出的,在这里ב是一个频率。这将返回一个值,代表频率ב㩦在原始信号中的普遍程度。反傅里叶变换由f(x)=∫-∞+∞f(x)e+2נixבdב给出。
问:傅里叶变换的输出是什么样子的?
答:傅里叶变换的输出可以被称为频谱或分布,因为它显示的是输入的可能频率的分布。
问:计算机是如何计算快速傅里叶变换的?
答:计算机使用一种叫做快速傅里叶变换(FFT)的算法来快速计算除最简单的信号的变换。
问:相对于时间看信号不能说明什么?
答:相对于时间看信号,并不能明显看出其中有哪些音符;许多信号如果把它们的频率分开并单独分析,反而更有意义。
搜索百科全书

