分形

例子

分形的类型很多，制作方式也很多样。其中一个例子是西尔宾斯基三角形，在这个大三角形内有无数个小三角形。另一个例子是曼德布罗特集，以Benoît Mandelbrot命名。西尔宾斯基三角形是用图案构建的，但曼德布罗特集是基于一个方程的。

自然界中也有许多分形的例子，包括树木、雪花、一些蔬菜和海岸线。

科赫曲线

科赫曲线是分形的一个简单例子。首先，从一条直线的一部分开始--称为直线段。将该线段切成3个同样大小的片段。去掉中间的部分，然后放入一个三角形的上半部分，其边长与要切掉的部分相同。我们现在有4条线段，它们的两端是相通的。我们现在可以对4个比特中的每一个做我们刚才对第一个线段所做的事情。现在我们可以对所有的位子重复做同样的事情。我们现在永远这样做，看看我们最后得到了什么。

科赫曲线的长度是无限的，而科赫曲线的面积是零。这是很奇怪的。一条线段（维数为1）可能有1的长度，但它的面积为0。一个长为1，宽为1的正方形（维数为2）将有1的面积和无穷的长度。

相似性维度

因此，科赫曲线似乎比维度1的东西大，而比维度2的东西小。相似性维度的概念是为了给分形的长度或面积提供一个更好的概念。因此，对于科氏曲线，我们希望维度在1到2之间。

科赫曲线可以被切割成四块，每块都是原始大小的1 3 {displaystyle {frac {1}{3}}} 。我们把一个分形可以切成的片数称为N {displaystyle N} ，我们把大小差异称为B {displaystyle B} 。我们把这些放入方程。

log N - log B {displaystyle {frac {log N}{-log B}}}。

其中log {displaystyle log } 是一个数字的对数。这个数字是分形的Hausdorff维度。在科赫曲线中，这就是log 4 - log 1 3 = 1.2619...{displaystyle {frac {log 4}{-log {frac {1}{3}}}}=1.2619...} ，因为我们想。

科赫曲线是最简单的分形之一，因此它的维数很容易算出来。它的相似性维度和Hausdorff维度都是一样的。但对于更复杂的分形来说，这就不是真的了。

科赫雪花

科赫雪花（或科赫星）与科赫曲线相同，只是它以一个等边三角形而不是线段开始。

如何制作科赫曲线

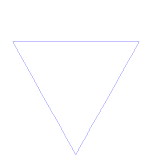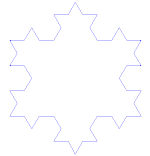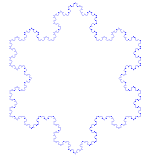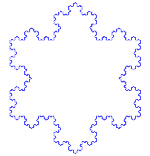
使用

分形有许多应用，例如在生物学（肺、肾、心率变异等）、地震、金融学（与所谓的重尾分布有关）和物理学中。这表明应该对分形进行研究，以了解为什么分形在自然界如此频繁。

有些分形只是出于艺术原因而存在，但其他分形却非常有用。分形是无线电天线非常有效的形状，在计算机芯片中被用来有效连接所有部件。另外，海岸线也可以被认为是分形。