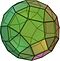
阿基米德立體
在几何学中,阿基米德实体是一种由多边形组成的凸形。它是一个多面体,具有以下特性。
- 每个面都是由一个规则的多边形组成
- 形状的所有角落看起来都一样
- 这种形状既不是柏拉图式的实体,也不是棱镜,更不是反棱镜。
根据不同的计算方式,有13或15个这样的形状。在这些形状中,有两个版本,不能用旋转的方式使之全等。阿基米德实体是以古希腊数学家阿基米德命名的,他可能在公元前3世纪发现了这些实体。阿基米德的著作已经失传,但亚历山大的帕普斯在4世纪总结了这些著作。在文艺复兴时期,艺术家和数学家重视纯粹的形式,重新发现了所有这些形式。约翰内斯-开普勒可能在1620年左右完成了这一探索。
构建一个阿基米德实体至少需要两个不同的多边形。
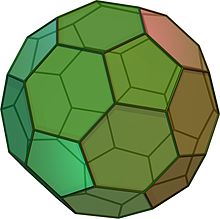
截断的二十面体看起来像一个足球。它是由12个等边五角形和20个正六边形组成。它有60个顶点和90条边。它是一个阿基米德实体
属性
- 阿基米德实体是由规则的多边形组成的,因此所有的边都有相同的长度。
- 所有阿基米德实体都可以从柏拉图实体中产生,方法是 "切割柏拉图实体的边缘"。
- 多边形在一个角上相遇("顶点")的类型,是阿基米德和柏拉图实体的特征。
与柏拉图实体的关系
通过遵循一系列的构造规则,柏拉图实体可以变成阿基米德实体。
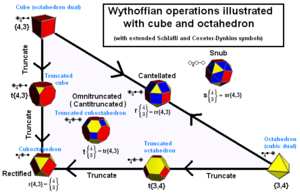
阿基米德固体可以被构建为万花筒中的发电机位置
阿基米德实体列表
以下是所有阿基米德实体的列表
| 图片 | 命名 | 脸部 | 类型 | 边缘 | 纬度 |
|
| 截断的四面体 | 8 | 4个三角形 4个六边形 | 18 | 12 |
|
| 14 | 8个三角形 6个方块 | 24 | 12 | |
|
| 截断的立方体 | 14 | 8个三角形 6个八角形 | 36 | 24 |
|
| 截断的八面体 | 14 | 6个方块 8个六边形 | 36 | 24 |
|
| 菱形正八面体 | 26 | 8个三角形 18个方块 | 48 | 24 |
|
| 截断的立方八面体 | 26 | 12个方块 8个六边形 6个八角形 | 72 | 48 |
|
| 斯诺布方块(2个镜像版本) | 38 | 32个三角形 6个方块 | 60 | 24 |
|
| 伊科斯十二面体 | 32 | 20个三角形 12个五角星 | 60 | 30 |
|
| 截断的十二面体 | 32 | 20个三角形 12个十元硬币 | 90 | 60 |
|
| 截断的二十面体 | 32 | 12个五角星 20个六边形 | 90 | 60 |
|
| 菱形十二面体 | 62 | 20个三角形 | 120 | 60 |
|
| 截断的二十二面体 | 62 | 30个方块 20个六边形 12个十元硬币 | 180 | 120 |
|
| 蛇形十二面体(2个镜像版本) | 92 | 80个三角形 12个五角星 | 150 | 60 |
问题和答案
问:什么是阿基米德实体?答:阿基米德实体是一种由多边形组成的凸形,其特性是每个面都是规则的多边形,所有的角都是一样的,而且不是柏拉图实体、棱镜或反棱镜。
问:有多少个阿基米德实体?
答:根据计算方式的不同,有13个或15个阿基米德实体。
问:谁发现了阿基米德实体?
答:阿基米德实体是以古希腊数学家阿基米德的名字命名的,他可能在公元前3世纪发现了这些实体。
问:亚历山大的帕普斯对阿基米德的著作做了什么?
答:亚历山大的帕普斯在4世纪时总结了阿基米德关于阿基米德实体的著作。
问:为什么艺术家和数学家在文艺复兴时期重新发现了阿基米德实体?
答:在文艺复兴时期,艺术家和数学家看重纯粹的形式,而阿基米德实体被认为是纯粹的形式。
问:约翰内斯-开普勒是什么时候完成对所有阿基米德实体的寻找的?
答:约翰内斯-开普勒可能在1620年左右完成了对所有阿基米德实体的搜索。
问:构造一个阿基米德实体需要什么条件?
答:构造一个阿基米德实体至少需要两个不同的多边形。
搜索百科全书