光钟

光钟是展示狭义相对论基本特征的一种简单方式。时钟的工作原理是，将一束光从远处的镜子上弹出，并利用它的回波触发另一束光，同时计算沿途发生了多少次闪光。很容易证明，地球上的人用这样的时钟看宇宙飞船从头顶飞过，会看到它的滴答声相对缓慢。这种效应叫做时间膨胀。

在研究光钟之前，先考虑另一种相对论。想象一下，有人在一架大型货机的机舱里运球。篮球运动员的运动方向与喷气式飞机的运动方向相同。飞机上的其他人看到他在运球时移动了一两米。从球第一次弹跳到球第二次弹跳之间，大约过了一秒钟。但是当第一次弹跳发生时，篮球是在直布罗陀上空，而当第二次弹跳发生时，篮球是在靠近西班牙的水面上。所以，篮球相对于地球已经移动了280米。

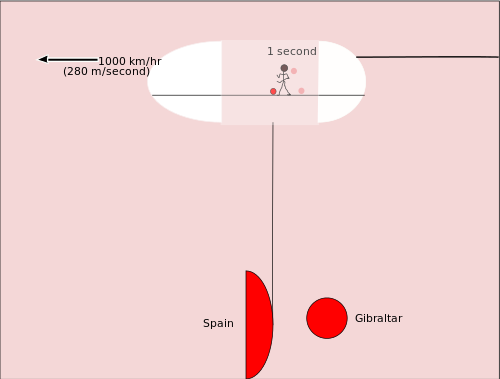
现在考虑一个有点类似的相对运动问题。这次我们要考虑的是，当一艘非常快的飞船飞过北极时，从北极看星星的人看到了什么。我们可以用代数和毕达哥拉斯定理来计算飞船上的时间慢了多少。我们唯一需要的是将距离d、速度r和时间t联系起来的方程式，这个方程式是：

d = rt

光速是恒定的，所以我们将把这个值应用到两个问题上。我们将把光速称为c，因为这是科学家通常用来命名的字母。

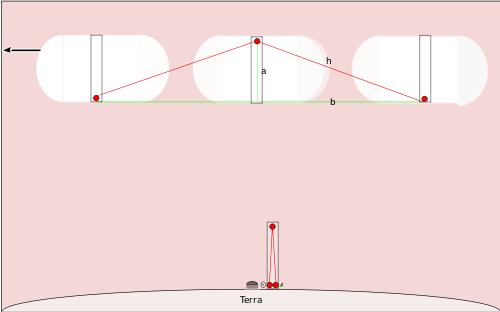
时钟的制作方法是在一根长杆的底部放一个光输出，杆顶放一面镜子，杆底放一个电子光检测器。启动时钟的方法是短暂地闭合一个开关，将一闪一闪的光从杆底送到杆顶，再反射到杆底。当杆子底部的光检测器看到光的闪烁时，它会做两件事。它把一束光加到与它相连的计数器上，并向镜子发射另一束闪烁的光。当那一闪的光回到底部时，计数就变成了二，再放出一闪的光。由于光的传播速度非常快（30万公里/秒），所以普通时钟每测量一秒，光钟就会"滴答"一次，次数非常多。

为了让数学更简单，我们就说北极点有半公里长。因此，如果我们站在建在北极大望远镜旁边的光钟旁，我们会看到光钟每"滴答"一声，光就走了一公里。由于走过的距离d等于速度乘以时间，而涉及到的速度是c，我们就有了这样的公式。

d = ct

我们可以解出t这个方程，以了解每个"滴答"的时间，以秒为单位。

1公里=300,000公里/秒*t秒

t秒=1公里/30万(公里/秒)=1/30万秒=0.00000333...3秒。

换句话说，光钟的每一次"滴答"都需要0.00000333...3秒。

如果一艘宇宙飞船以直线飞行，以很大一部分光速经过北极点，而且它有一个类似的时钟，观察它经过的人就会看到，北极点顶部的镜子已经从发射光的正上方移动了，所以光会沿着图中标有h的线传播，然后它会沿着另一个次方回到北极点的底部--由于宇宙飞船移动得太快，现在已经移动了一段距离。我们可以根据地球上的人计算出一个刻度需要多少时间。我们知道飞船的极点的长度是a，因为它和人们在北极使用的时钟是一样的。我们要算出t'，就是飞船上的时钟滴答一次所需的时间。

我们知道，当眨眼的光向镜面上行时，飞船将行驶1/2 r t'，当眨眼的光向极点底部下行时，飞船又将行驶1/2 r t'。所以，这样计算就得到了图中b线的长度。我们知道了a，所以我们可以通过毕达哥拉斯定理计算出h。

h = √(^a2 + (rt' /2)²)

所以光的总路程为2小时或d=2√(^a2+(rt' /2)²)

我们还知道，光速c是恒定的。无论谁来测量，结果都是一样的速度。因此，我们可以利用这一事实，得到另一种计算方法，即计算闪光从极点底部到极点顶部再到极点的时间。

t'=d/c

换句话说，d=c t'。

所以我们可以写

c t' = 2 √(^a2 + (rt' /2)²)

或

1/2 c t' = √(^a2 + (rt' /2)²)

要解上述方程，我们需要。

1. 两边方形
2. 两边除以t'²
3. 两边都乘以4
4. 两边除以^c2
5. 简化^c2/^c2
6. 从两边减去^r2/^c2
7. 取两边的平方根
8. 两边都乘以t'。
9. 两边都除以√（1-^r2/^c2）。

解开上式，我们发现。

t'=2a/(c√(1-^r2/^c2)

北极的时钟上的刻度之间的时间是2a/c，所以我们可以写出：

t' = t/√(1-^r2/^c2)

如果t=1秒，那么如果飞船以二分之一的光速飞行，t'=1.1547秒。

实验各种行进速度：http://www.1728.org/reltivty.htm。

问题和答案

按字母搜索