平行公设
在几何学中,平行公设是欧几里得几何学的公理之一。有时它也被称为欧几里德第五公设,因为它是欧几里德《元素》中的第五公设。
该公设说,。
如果你用两条线切开一条线段,而线段形成的两个内角加起来小于180°,那么如果你把它们延长到足够长的时间,这两条线最终会相遇。
遵循欧几里得所有公理的几何学领域被称为欧几里得几何学。不遵循欧几里得所有公理的几何学被称为非欧几里得几何学。
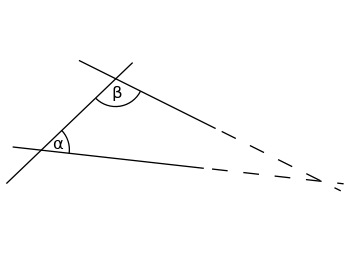
如果内角α(α)和β(β)的总和小于180°,这两条线将在某处相交,如果这两条线都被延长到无限长。
历史
一些数学家认为,欧几里得的第五条公设比其他四条公设长得多,也复杂得多。他们中的许多人认为,它可以从其他较简单的公理中得到证明。一些数学家宣布他们已经从较简单的命题中证明了这个命题,但他们都被证明是错误的。
普莱菲尔公理
另一个较新的命题被称为普莱菲尔公理,与欧几里德的第五公设相似。它说。
给定一条直线和一个不在这条直线上的点,你只能画一条通过这个点的直线,而这个点不会与另一条直线相遇。
事实上,数学家们发现,这个公理不仅与欧几里德的第五公设相似,而且具有完全相同的含义。在数学上,这两个命题被称为 "等价 "命题。今天,普莱菲尔公理比欧几里德的原始平行公设更经常被数学家使用。
非欧几里得几何学
最终,一些数学家试图在不使用公理的情况下建立新的几何学。一种非欧几里得几何学被称为椭圆几何学。在椭圆几何中,平行公设被一个公理所取代,该公理指出:。
给定一条直线和一个不在这条直线上的点,你不可能画出一条通过这一点而最终不穿过另一条直线的直线。
数学家们发现,当他们用这个公理取代欧几里德的第五公设时,他们仍然能够证明欧几里德的许多其他定理。想象椭圆几何的一种方法是通过思考地球仪的表面。在地球仪上,经线在赤道上似乎是平行的,但它们都在两极相遇。在19世纪末,椭圆几何学被证明是一致的。这证明欧几里德的第五条公设并不独立于其他公设。此后,数学家们大多不再试图从其他四条公设中证明第五条公设。相反,许多数学家开始研究不遵循欧几里德第五公设的其他几何学。
数学家们有时用另一条公理来代替欧几里德的第五条公理说。
给定一条直线和一个不在这条直线上的点,你可以画出至少两条通过这一点的直线,这些直线最终不会与另一条直线相交。
这就是所谓的双曲几何。
另一种几何学只是删除了欧几里德的第五公设,并没有用任何东西来取代它。这被称为中性几何学或绝对几何学。
搜索百科全书