標準差
标准差是一个数字,用于说明一个群体的测量结果与平均数(平均值)或预期值的分布情况。低标准差意味着大多数数字都接近于平均值。高标准差意味着数字更加分散。
报告的误差率通常是标准偏差的两倍。科学家们通常报告实验中数字与平均数字的标准差。他们经常决定,只有大于标准差两到三倍的差异才是重要的。标准差在货币方面也很有用,利息收入的标准差显示了一个人的利息收入与平均水平的差异。
很多时候,只能测量一个样本,或一个群体的一部分。那么,可以通过一个稍有不同的方程式找到一个接近整个群体的标准差的数字,这个方程式叫做样本标准差,下面会解释。
.png)
正态分布(或钟形曲线)的图。每个色带的宽度为一个标准差。
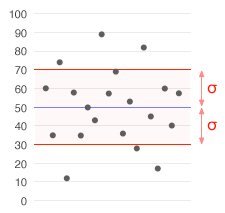
一个平均数为50的数据集(以蓝色显示),标准差(σ)为20。
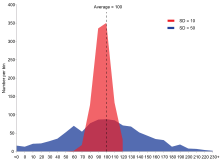
具有相同平均值和不同标准偏差的两个样本人口的例子。红色人口的平均数为100,SD为10;蓝色人口的平均数为100,SD为50。
基本例子
考虑一个有以下八个数字的小组。
2, 44,4 , , 55, {displaystyle 2, 4, 4, 4, 5, 5,79 7, 9}.
这八个数字的平均数(平均值)为5。
2+ 44+ 4+ 5+ 57= {displaystyle {frac {2+4+4+4+5+5+7+9}{8}=5985}。
要计算人口标准差,首先要找出列表中每个数字与平均值的差。然后将每个差值的结果平方。
(2 -5 ) =2 ( - 3) = 2(95 -5 ) = 2( 04- ) 52=02 ( - 1) = 202(1504 - 55) 2= ( - ) = 22(17 - ) = ( - 15) = ( - ) 2= 22( 44- 51) = 22(19 - 5) 2= {\4216displaystyle {begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}
接下来,找出这些数值的平均值(总和除以数字的数量)。最后,取其平方根。
( +9 + 1+1 + 10+ 04)16 = {\82displaystyle {sqrt {frac {(9+1+1+0+0+4+16)}{8}=2}.
答案是人口标准差。只有当我们开始的八个数字是整个群体的时候,这个公式才是正确的。如果它们只是随机抽取的一部分,那么我们应该在倒数第二步的底部(分母)使用7(即n-1)而不是8(即n)。那么答案就是样本标准差。这就是所谓的贝塞尔修正法。
更多的例子
一个稍微难一点的、现实生活中的例子。美国成年男子的平均身高为70英寸,标准偏差为3英寸。3 "的标准差意味着大多数男性(约68%,假设为正态分布)的身高比平均水平(67"-73")高3 "到3",即一个标准差。几乎所有男性(约95%)的身高都比平均值(64"-76")高6英寸到矮6英寸--两个标准差。三个标准差包括被研究的样本人口中99.7%的所有数字。如果分布是正常的(钟形),这就是真实的。
如果标准偏差为零,那么所有男人的身高都正好是70英寸。如果标准偏差为20英寸,那么有些男人会比平均水平高得多或矮得多,典型的范围大约为50英寸-90英寸。
再比如,{0,0,14,14}、{0,6,8,14}和{6,6,8,8}这三组的平均数(平均值)都是7,但是它们的标准差是7、5和1。第三组的标准差比其他两组小得多,因为它的数字都接近于7。基本概念是,标准差告诉我们其余的数字离平均值有多远。它的单位与数字本身相同。例如,如果{0,6,8,14}组是一组四兄弟的年龄,平均为7岁,标准偏差为5岁。
标准差可以作为不确定性的一个衡量标准。例如,在科学中,一组重复测量的标准偏差可以帮助科学家了解他们对平均数的把握程度。当决定一个实验的测量值是否与预测值一致时,这些测量值的标准差是非常重要的。如果实验的平均数与预测数相差太远(以标准差衡量的距离),那么被测试的理论可能不正确。见预测区间。
应用实例
了解一组数值的标准差的作用在于知道与 "平均数"(mean)的预期差异有多大。
天气
作为一个简单的例子,考虑两个城市的平均日最高气温,一个在内陆,一个在海洋附近。了解靠近海洋的城市的日最高温度范围比内陆城市小是有帮助的。这两个城市可能各自有相同的日平均高温。然而,沿海城市的日最高温度的标准偏差将小于内陆城市。
体育
另一种方法是考虑运动队。在任何运动中,都会有一些团队擅长一些事情,而在其他方面则不擅长。排名最高的球队在能力上不会表现出很大的差异。他们在大多数类别中都做得很好。他们在每个类别中的能力的标准差越低,他们就越平衡和稳定。然而,标准差越高的球队,其可预测性就会越低。一支通常在大多数类别中都很差的球队将有一个低标准差。一个通常在大多数类别中表现良好的球队也会有一个低的标准差。然而,一个标准差高的球队可能是那种得分多(进攻强)但也让其他球队得分多(防守弱)的球队。
试图提前知道哪些球队会赢,可能包括查看各种球队 "统计数字 "的标准偏差。与预期不同的数字可以匹配优势与劣势,以显示哪些原因可能对知道哪支球队将获胜最为重要。
在赛车中,车手完成每一圈的时间被衡量。单圈时间标准偏差小的车手比标准偏差大的车手更稳定。这一信息可以用来帮助了解车手如何减少完成一圈的时间。
奖金
在货币中,标准差可能意味着一个价格将上升或下降的风险(股票、债券、房产等)。它也可以意味着一组价格将上升或下降的风险(主动管理的共同基金,指数共同基金,或ETF)。风险是决定买什么的一个原因。风险是人们可以用来知道他们可能赚取或损失多少钱的一个数字。随着风险变大,一项投资的回报可能超过预期("加 "标准差)。然而,一项投资也可能比预期损失更多的钱("负 "标准差)。
例如,一个人不得不在两只股票中做出选择。在过去20年里,股票A的平均回报率为10%,标准差为20个百分点(pp)。股票B在过去20年的平均回报率为12%,但标准差较高,为30个百分点。考虑到风险,这个人可能决定股票A是更安全的选择。尽管他们可能赚不到那么多钱,但他们可能也不会损失很多钱。这个人可能认为,股票B的平均收益高出2个百分点,不值得增加10个百分点的标准差(预期收益的风险或不确定性更大)。
正态分布数的规则
大多数标准差的数学公式都假定数字是正常分布的。这意味着数字以某种方式分布在平均值的两边。正态分布也被称为高斯分布,因为它是由卡尔-弗里德里希-高斯发现的。它通常被称为钟形曲线,因为数字分散开来,在图形上呈现出钟形的形状。
如果数字被分组在平均值的一侧或另一侧,就不是正态分布。数字可以分散,但仍然是正态分布。标准差告诉我们数字分布的范围有多大。

深蓝色是指与平均值相差不到一个标准差。对于正态分布来说,这包括68.27%的数字;而与平均值的两个标准差(中等和深蓝色)包括95.45%;三个标准差(浅、中、深蓝色)包括99.73%;而四个标准差占99.99%。
平均数(平均值)和标准差的关系
一组数据的平均数(平均值)和标准差通常写在一起。然后一个人就可以理解平均数是多少,以及这组数据中其他数字的分布情况。
一组数字的分布方式也可以由变异系数给出,即标准差除以平均值。它是一个无尺寸的数字。变异系数通常被乘以100%,并写成百分比。
历史
卡尔-皮尔逊(Karl Pearson)在1894年首次在书面上使用标准差这个词,此前他在讲座中使用过这个词。它是作为对同一概念的早期名称的替代:例如,高斯使用了平均误差。
相关页面
- 准确度和精确度
- 样本数量
问题和答案
问:什么是标准差?答:标准差是一个数字,用于说明一个群体的测量值与平均值(平均值或预期值)的分布情况。
问:低标准差是什么意思?
答:低标准差意味着大多数数字都接近于平均值。
问:高标准差是什么意思?
答:高标准差意味着数字更加分散。
问:标准差在货币中是如何使用的?
答:在货币中,利息收入的标准差表明一个人的利息收入可能与平均水平有多大差别。
问:什么时候可以只对一个群体的一部分进行测量?
答:很多时候,只能测量一个样本,或一个群体的一部分。
问:整个群体的标准差是如何表示的?
答:整个组的标准差是由希腊字母 َ {displaystyle \sigma }表示的。.
问:样本的标准差是如何表示的?
答:样本的标准差用s表示 {{displaystyle s} 。
搜索百科全书



