维恩图
维恩图是一种显示集合之间逻辑关系的图示。它们由约翰-维恩在19世纪80年代推广,现在被广泛使用。它们被用来教授初级集合理论,以及说明概率、逻辑、统计、语言学和计算机科学中的简单集合关系。维恩图使用平面上的封闭曲线来表示集合。这些曲线通常是圆或椭圆。
在文恩之前也有人提出过类似的想法。Christian Weise在1712年(Nucleus Logicoe Wiesianoe)和Leonhard Euler(Letters to a German Princess)1768年都提出了类似的想法。这个想法被维恩在《符号逻辑》中推广,第五章 "图解表示",1881年。

剑桥的彩色玻璃窗,约翰-文恩在那里学习。它显示了一个维恩图。
例子
下面的例子使用了两个集合,A和B,这里用彩色的圆圈表示。橙色的圆圈,即A组,代表所有两腿的生物。蓝色的圆圈,即集合B,代表可以飞行的生物。每种不同类型的生物都可以被想象成图中某处的一个点。既能飞又有两条腿的生物--例如鹦鹉--都在两个集合中,所以它们对应于蓝色和橙色圆圈重叠的区域中的点。这个区域包含所有这样的生物,也只有这样的生物。
人类和企鹅是两足动物,所以就在橙色的圆圈里,但是因为他们不能飞,所以他们出现在橙色圆圈的左边部分,与蓝色圆圈不重叠的地方。蚊子有六条腿,会飞,所以蚊子的点是在蓝色圆圈中与橙色圆圈不重叠的部分。那些没有两条腿也不会飞的生物(例如鲸鱼和蜘蛛)都会用两个圆圈以外的点来表示。
集合A和B的面积称为A和B的联合体,用A∪B表示。在这种情况下,联合体包含所有两腿或会飞(或两者)的生物。A和B两个集合重叠的区域称为A和B的交点,用A∩B表示。例如,这两个集合的交点不是空的,因为有一些点代表了同时处于橙色和蓝色圆圈中的生物。
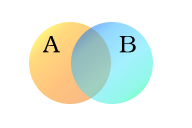
A组(有两条腿的生物)和B组(能飞的生物)。
问题和答案
问:什么是维恩图?答:维恩图是一种显示集合之间逻辑关系的图。它用画在平面上的封闭曲线,通常是圆或椭圆,来表示集合。
问:谁推广了维恩图?
答:约翰-文恩在19世纪80年代推广了文恩图。
问:它们的用途是什么?
答:它们被用来教授初级集合理论,并说明概率、逻辑、统计、语言学和计算机科学中的简单集合关系。
问:在约翰-文恩之前,谁提出了类似的想法?
答:Christian Weise在1712年以他的Nucleus Logicoe Wiesianoe提出了类似的想法,Leonhard Euler在1768年给一位德国公主的信中提出了这些想法。
问:约翰-文恩是什么时候发表《符号逻辑》的?
答:约翰-文恩在1881年出版了《符号逻辑》。
问:约翰-文恩在《符号逻辑》的哪一章中推广了文恩图的概念?
答:维恩图的概念是由约翰-维恩在《符号逻辑》第5章 "图解表示法 "中推广的。
问:在现代版文恩图发明之前,这些思想是如何表现的?
答:在现代版V enn图发明之前,这些思想是用画在平面上的封闭曲线表示的,如圆或椭圆。
搜索百科全书