指数函数
在数学中,指数函数是一个迅速增长的函数。更确切地说,它是函数exp ( x ) = e x {displaystyle \exp(x)=e^{x}} ,其中e是欧拉常数,是一个大约2.71828的无理数。
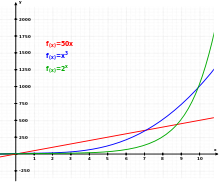
三个不同的函数。线性(红色)、立方(蓝色)和指数(绿色)。
属性
因为指数函数使用指数化,所以它们遵循同样的规则。因此:
exp ( x + y ) = exp ( x ) exp ( y ) = e x + y {displaystyle xp(x+y)=exp(x)\exp(y)=e^{x+y}}。

自然对数是指数函数的逆运算。
ln ( x ) = log e ( x ) = log ( x ) log ( e ) {displaystyle ln(x)=log _{e}(x)={frac {log(x)}{log(e)}}.
指数函数在微分计算中满足一个有趣和重要的属性。
d d x e x = e x {displaystyle {frac {mathrm {d} }{mathrm {d} x}}e^{x}=e^{x}}.}{mathrm {d} x}}e^{x}=e^{x}}。
这意味着指数函数的斜率是指数函数本身,随后这意味着它在x={0displaystyle x=0}
应用程序
指数函数是最有用的数学函数之一。它被用来表示指数增长,几乎在所有科学科目中都有应用,在金融学中也很突出。指数衰变也会发生,例如放射性衰变和光的吸收。
指数函数在现实生活中的一个例子是银行的利息。如果一个人把100英镑存入一个每月有3%利息的账户,那么每个月的余额将是(假设钱没有被动过)。
| 月份 | 平衡 | 月份 | 平衡 |
| 一月 | £100.00 | 七月 | £119.41 |
| 2月 | £103.00 | 八月 | £122.99 |
| 三月 | £106.09 | 9月 | £126.68 |
| 四月 | £109.27 | 10月 | £130.48 |
| 5月 | £112.55 | 11月 | £134.39 |
| 6月 | £115.93 | 12月 | £138.42 |
注意来自利息的额外资金是如何逐月增加的。原始余额越大,这个人得到的利息就越多。
下面是两个指数函数的数学例子。
| a=2
| a=3
|
与数学常数e的关系
尽管基数(a {displaystyle a}
数字e对每个指数函数都很重要。例如,一家银行每天支付0.01%的利息。一个人拿着他的利息钱,放在一个盒子里。10000天后(约30年),他的钱是他开始时的2倍。另一个人拿着他的利息钱,把它放回银行。因为银行现在向他支付利息,钱的数量是一个指数函数。10000天后,他的钱不是他开始时的2倍,但他的钱是他开始时的2.718145倍。这个数字非常接近数字e。如果银行支付利息的频率更高,所以每次支付的金额更少,那么这个数字将更接近数字e。
一个人也可以通过看图片来了解为什么数字e对指数函数很重要。图中有三条不同的曲线。有黑点的曲线是一个基数比e小一点的指数函数。有黑色短线的曲线是一个基数比e大一点的指数函数。它在一个点上与蓝色曲线相接触,但没有越过它。人们可以看到,红色曲线在-1处与X轴(从左到右的直线)相交,只有蓝色曲线是这样的。这就是以e为基数的指数函数很特别的原因。
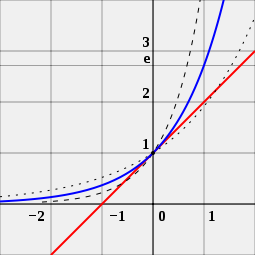
e 是唯一的数字a,使指数函数f(x)=ax(蓝色曲线)在x=0点的导数值正好是1。为便于比较,图中显示了函数2x(虚线)和4x(虚线);它们与斜率为1(红色)的直线不相切。
问题和答案
问:什么是指数函数?答:指数函数是一种增长速度越来越快的数学函数。
问:指数函数在数学上是如何表达的?
答:指数函数在数学上表示为exp(x) = e^x,其中e是欧拉常数。
问:欧拉常数代表什么?
答:欧拉常数代表一个无理数,约为2.71828。
问:指数函数是否总是在增加?
答:是的,指数函数的值总是随着x的增加而增加。
问:指数函数的增长速度有什么限制吗?
答:没有,指数函数的增长速度没有限制,因为它随着x值的增大而继续增加。
问:我们怎样才能计算欧拉常数?
答:我们可以用泰勒级数或续分数等数字方法来计算欧拉常数。
问:除了数学以外,指数函数还有哪些应用?
答:指数函数在数学之外还有很多应用,包括物理学、化学、生物学、经济学和工程学。
搜索百科全书

