四色定理

问题的准确表述

直观地说，四色定理可以表述为'给定一个平面的任何分隔为相邻的区域，称为地图，这些区域最多可以使用四种颜色进行着色，使相邻的两个区域没有相同的颜色'。为了能够正确解决这个问题，有必要澄清一些方面的问题。首先，所有属于三个或更多国家的点必须被忽略。第二，区域面积有限而周长无限的奇异地图可能需要四种以上的颜色。

就该定理而言，每一个"国家"都必须是一个简单连接的区域，或者说是毗连的区域。在现实世界中，情况并非如此。阿拉斯加是美国的一部分，纳希切万是阿塞拜疆的一部分， 加里宁格勒是俄罗斯的一部分，这些都不是毗连的。因为某个国家的领土必须是相同的颜色，四种颜色可能不够。例如，考虑一个简化的地图，如左图所示。在这张地图上，标有A的两个地区属于同一个国家，而且必须是同一种颜色。那么这张地图就需要五种颜色，因为A两个区域一起与其他四个区域相邻，每个区域都与其他所有区域相邻。如果A只有三个区域，可能需要六种或更多的颜色。这样一来，就可以做出需要任意多的颜色的地图。如果所有的水体都使用一种颜色，类似的结构也适用于真实地图。

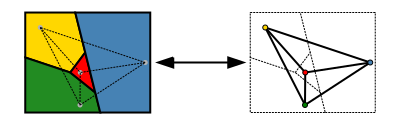
该定理的一个更容易说明的版本使用图论。地图的区域集可以更抽象地表示为一个无向图，该图的每个区域都有一个顶点，每一对共享边界线的区域都有一条边。这个图是平面的：它可以在平面上无交叉地绘制，方法是将每个顶点放在它所对应的区域内任意选择的位置，并将边绘制成曲线，在每个区域内无交叉地从顶点位置通向该区域的每个共享边界点。反之任何平面图都可以用这种方式由地图形成。在图论术语中，四色定理指出，每个平面图的顶点最多可以用四种颜色来着色，因此没有两个相邻的顶点具有相同的颜色，或者简而言之，"每个平面图都是可以四色的"(Thomas 1998, p. 849; Wilson 2002)。

带有非毗连地区的阿塞拜疆地图示例。


此地图不能用四种颜色着色

历程

第一个提出这个问题的人是弗朗西斯-格斯里，在1852年。他当时是英国的一名法律系学生，。他发现，他需要至少四种颜色来给英国各郡的地图上色。奥古斯都-德-摩根第一次讨论这个问题，是在1852年8月他写给罗文-哈姆利顿的一封信中。在信中，德-摩根问道，四种颜色是否真的足够给地图上色，以至于相邻的国家得到的颜色都不一样。

英国数学家Arthur Cayley在1878年向伦敦的数学协会提出了这个问题。一年之内，阿尔弗雷德-肯普找到了这个问题的证明。11年后，在1890年，Percy Heawood证明了Alfred的证明是错误的。彼得-格斯里-泰特在1880年提出了另一个证明的尝试。花了11年时间，证明泰特的证明也没有成功。1891年，朱利叶斯-彼得森可以证明这一点。当他伪造了凯利的证明时，凯姆普也展示了一个问题的证明，他称之为五色定理。该定理说，任何这样的地图可以用不超过五种颜色来着色。有两个限制条件。首先，任何一个国家都是连续的，没有exclaves。第二个限制是，国家需要有一个共同的边界，如果它们只在一个点上接触，就可以用同一种颜色来着色。尽管Kempe的证明是错误的，但他使用了一些后来允许正确证明的想法。

在20世纪60年代和70年代，Heinrich Heesch开发了第一个用计算机证明的草图。Kenneth Appel和Wolfgang Haken在1976年改进了这个草图（Robertson等人，1996年）。他们能够将需要测试的案例数量减少到1936个；后来又做出了一个版本，只依靠测试1476个案例。每个案例都需要用计算机进行测试（Appel和Haken，1977年）。

1996年，尼尔-罗伯逊、丹尼尔-桑德斯、保罗-西摩和罗宾-托马斯改进了这一方法，将需要测试的案例数量减少到663个。同样，每个案例都需要用计算机进行测试。

2005年，Georges Gonthier和Benjamin Werner开发了一个正式证明。这是一个进步，因为它第一次允许使用定理证明软件。使用的软件叫做Coq。

四色定理是第一个借助计算机证明的数学大问题。由于这个证明不能由人完成，所以一些数学家不承认它的正确性。要验证这个证明，就必须依靠正确工作的软件和硬件来验证这个证明。因为证明是由计算机完成的，所以也不是很优雅。

结果是错误的尝试

四色定理在漫长的历史中，因为吸引了大量的错误证明和反证而臭名昭著。起初，《纽约时报》拒绝报道阿佩尔-哈肯证明。该报这样做是出于政策考虑，它担心这个证明会像之前的证明一样被证明是假的（Wilson 2002，第209页）。有些证明需要很长的时间，直到它们可以被伪造。就Kempe和Tait的证明而言，伪造它们花了十多年时间。

最简单的反例通常试图创建一个区域，该区域触及所有其他区域。这就迫使其余区域只能用三种颜色来着色。由于四色定理是真实的，这总是可能的；但是，由于绘制地图的人专注于一个大的区域，他们没有注意到其余的区域实际上可以用三种颜色来着色。

这个技巧可以推广。如果事先选择了地图中某些区域的颜色，就不可能给其余区域上色，使其总共只使用四种颜色。有人在验证反例时，可能不会想到可能需要改变这些区域的颜色。这将使反例看起来是有效的，即使它不是。

也许这种常见的误解背后的一个影响是，颜色限制不是反转性的：一个区域只需要与它直接接触的区域有不同的颜色，而不是接触它所接触的区域的区域。如果是这样的限制，平面图形将需要任意多的颜色。

其他错误的反证以意想不到的方式违反了定理的假设，比如使用一个有多个不相连的区域，或者不允许相同颜色的区域在某一点上接触。

着色政治地图

在现实生活中，很多国家都有exclaves或殖民地。由于它们属于国家，所以需要用与母国相同的颜色来着色。这意味着，通常情况下，需要四种以上的颜色来给这样的地图上色。当数学家谈论与问题相关的图形时，他们说那不是平面的。尽管检查一个图形是否是平面的很容易，但找到给它上色所需的最少的颜色数量是非常困难的。它是NP-完备的，这是最困难的问题之一。给一个图形上色所需的最少颜色数被称为它的色数。在试图解决四色定理时发生的许多问题都与离散数学有关。为此，经常使用代数拓扑学的方法。

扩展到"非平面"地图

四色定理要求"地图"在一个平面上，也就是数学家所说的平面。1890年，Percy John Heawood创造了今天被称为Heawood猜想的东西。它提出了与四色定理相同的问题 但适用于任何拓扑对象。举个例子，一个环形物最多可以有七种颜色。Heawood猜想给出了一个适用于所有此类对象的公式，除了克莱因瓶。