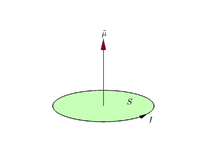
磁矩

矩的两个定义

在教科书中，有两种互补的方法被用来定义磁矩。在1930年以前的教科书中，它们是用磁极来定义的。最近的教科书则用安培拉电流来定义它。

磁极定义

物理学家将材料中的磁矩来源表示为两极。南北两极与静电学中的正负电荷相类似。考虑一个条形磁铁，它的磁极大小相同但极性相反。每一个磁极都是磁力的来源，随着距离的增加而减弱。由于磁极总是成对出现，它们的力量部分地相互抵消，因为当一个磁极拉动时，另一个磁极则排斥。当两极相互靠近时，即当条形磁铁较短时，这种抵消作用是最大的。因此，由条形磁铁产生的磁力，在空间的某一点上，取决于两个因素：一是其磁极的强度p {displaystyle p}，二是分离它们的矢量l {displaystyle mathbf {l}。}将它们分开。矩被定义为

m = p l .{displaystyle {m} =p\mathbf {l} .}

它指向从南极到北极的方向。与电偶极的类比不应该走得太远，因为磁偶极与角动量有关（见磁矩和角动量）。尽管如此，磁极对于磁静力学的计算非常有用，特别是在铁磁体的应用中。使用磁极方法的实践者通常用非旋转场H {displaystyle\mathbf {H}表示磁场。}与电场E {displaystyle\mathbf {E}相类似。}.

电流环定义

假设一个平面闭合环路携带电流I {displaystyle I}，并具有矢量面积S {displaystyle \mathbf {S}。}( x {displaystyle x} , y {displaystyle y} , and z {displaystyle z} ) 。这个矢量的坐标是环路投射到y z {displaystyle yz}、z x {displaystyle yz}和z {displaystyle z}的面积。，z x {displaystyle zx}和x y {displaystyle zx}的投影面积。和x y {displaystyle xy}平面）。它的磁矩m {displaystyle \mathbf {m} {displaystyle \mathbf {m}}是指它的磁矩。}，矢量，被定义为。

m = I S .{displaystyle {m} =I\mathbf {S} .}

按照惯例，矢量区的方向是由右手握力法则给出的（将右手的手指沿着电流的方向绕圈，当手掌 "接触 "到圈的外缘时，直的拇指表示矢量区的方向，从而表示磁矩的方向）。

如果环路不是平面的，那就给定扭矩为

m = I 2∫ r × d r 。{displaystyle {mathbf {m} ={frac {I}{2}}int {mathbf {r}}。\times {rm {d}}\mathbf {r} 。}

在空间中任意电流分布的最一般情况下，这种分布的磁矩可以从以下公式中找到。

m = 12∫ r × J d V ，{displaystyle\mathbf {m} ={frac {1}{2}}int \mathbf {r} 。times\mathbf {J} ={frac {1}{2}int\mathbf {r}.\V,}，{rm {d}}V,}。

其中r {displaystyle `mathbf {r}是指从原点指向体积元素位置的位置矢量。}是指从原点到体积元素位置的位置矢量，而J {displaystyle\mathbf {J}}是该位置的电流密度矢量。}是该位置的电流密度矢量。

上述公式可用于计算任何运动电荷组合的磁矩，如旋转的带电固体，代之以

J = ρ v , {displaystyle \mathbf {J} =\rho \mathbf {v} , }

其中ρ {displaystyle \rho }是某一点的电荷密度，v {displaystyle \mathbf {v} }是该点的瞬时线速度。

例如，沿圆周运动的电荷所产生的磁矩为

m = q 12r × v {displaystyle \m} ={frac {1}{2}},q,\mathbf {r}}。\times \mathbf {v} } ，这是对的。,

其中r {displaystyle `mathbf {r}是电荷q {displaystyle q}相对于圆心的位置，v {displaystyle `mathbf {v}是电荷的瞬间速度。}是电荷q {displaystyle q}相对于圆心的位置，v {displaystyle `mathbf {v} }是电荷的瞬时速度。

使用电流环模型的实践者通常用螺线管场B来表示磁场 {displaystyle \mathbf {B}.}类似于静电场D {displaystyle\mathbf {D}}。}.

螺线管的磁矩

上述电流回路的概括是一个多圈线圈，或螺线管。它的力矩是各个匝数的力矩的矢量和。如果螺线管有N {displaystyle N}个相同的匝数（单层绕组）。

m = N I S 。{displaystyle {m} =NI\mathbf {S} .}

螺线管的3-D图像。


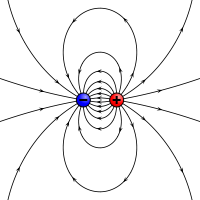
磁矩的静电类似物：两个对立的电荷相隔一个有限的距离。

单位

磁矩的单位在国际单位制（SI）中不是一个基本单位，它可以用多种方式表示。例如，在电流环定义中，面积以平方米为单位，I {displaystyle I}以安培为单位，所以磁矩以安培-平方米为单位( A m {\2displaystyle {text{A m}}^{2}} )。在力矩方程中，力矩以牛顿米为单位，磁场以特斯拉为单位，因此力矩以每特斯拉N.m为单位 ( N.m T -1 {\displaystyle {text{N.m T}}^{-1}} )。这两种表示法是等价的。

A m = 2N.m T - 1。{displaystyle {，{text{A m}}^{2}=，{text{N.m T}}^{-1}。}

在CGS系统中，有几套不同的电磁学单位，其中主要的有ESU、高斯和EMU。其中，在CGS中，有两个备选的（非等价的）磁偶极矩单位。

(ESU CGS) 1 statA-cm² = 3.33564095^-14×10 (m-²A 或 N.m/T)

和（更经常使用）的

(EMU CGS和Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10^-3 (m²-A或N.m/T)。

这两个非等价的CGS单位的比率（EMU/ESU）正好等于自由空间的光速，以cm/s表示。

本文的所有公式在SI单位中都是正确的，但在其他单位系统中，公式可能需要改变。例如，在SI单位中，一个电流为I、面积为A的电流环具有磁矩I×A（见下文），但在高斯单位中，磁矩为I×A/c。

一些基本粒子的内在磁矩和自旋
粒子	以SI单位计算的磁偶极矩（10 J/−27T）	自旋量子数（无尺寸）
电子	-9284.764	1/2
质子	14.106067	1/2
中子	-9.66236	1/2
介子	-44.904478	1/2
氘核	4.3307346	1
蚖虫	15.046094	1/2

关于磁矩和磁化的概念之间的关系，见磁化。