向量

例如,矢量将被用来显示某物移动的距离和方向。如果你问路,一个人说 "朝北走一公里",这就是一个向量。如果他说 "走一公里",但没有显示方向,这就是一个标量。
我们通常把向量画成箭头。箭头的长度与向量的大小成正比。箭头所指向的方向就是该向量的方向。
向量的例子
标量的例子
更多关于向量的例子
如何添加向量
使用从头到尾的方法在纸上添加向量
从头到尾的向量相加方法对于在纸上估算两个向量相加的结果很有用。要做到这一点。
- 每个向量都被画成一个箭头,后面有一定的长度,纸上的每一个长度单位代表向量的一定幅度。
- 绘制下一个矢量,第二个矢量的尾部(末端)位于第一个矢量的头部(前端)。
- 对所有其他矢量重复上述步骤。在前一个向量的头部绘制下一个向量的尾部。
- 从第一个向量的尾部到最后一个向量的头部画一条线,这就是所有向量的结果(总和)。
这被称为 "从头到尾 "的方法,因为前一个矢量的每个头都会导致下一个矢量的尾部。
使用组件形式
[需要解释的是 d]
使用分量形式将两个向量相加,从字面上看就是将两个向量的分量相加,形成一个新的向量。例如,让a和b是两个二维向量。这些向量可以用它们的分量来写。
a = ( a x , a y ) {\displaystyle\mathbf {a} =(a_{x},a_{y}) }
b = ( b x , b y ) {\displaystyle\mathbf {b} =(b_{x},b_{y}) }
假设c是这两个向量之和,所以c=a+b。这意味着c=( a x + b x , a y + b y ) {displaystyle\mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})}
下面是一个两向量相加的例子,使用它们的分量形式。
a = ( ,3 -1 ) {displaystyle\mathbf {a} =(3,-1)}。
b = ( ,2 ) {2displaystyle\mathbf {b} =(2,2)}。
c = a + b {displaystyle\mathbf {c} =\mathbf {a} +\mathbf {b} }}
= ( a x + b x , a y + b y ) {displaystyle =(a_{x}+b_{x},a_{y}+b_{y}) }
= ( + 3,2 - 1+ ) {2displaystyle =(3+2,-1+2) }
= ( ,5 ) {1displaystyle =(5,1)}
这种方法适用于所有的矢量,而不仅仅是二维的矢量。
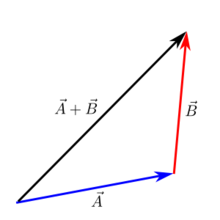
从头到尾的增加
如何进行向量相乘
使用点积
点积是一种向量相乘的方法。它产生一个标量。它使用分量形式。
a = ( , 2)3 b = ( ,1 ) 4a ⋅ b = ( , 2)3 ⋅ ( ,1 ) 4= ( 2⋅ ) 1+ ( 3⋅ )4 = +2 = {\1214displaystyle {\begin{aligned}\mathbf {a} =(2。3)\mathbf {b} =(1,4)\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\=(2\cdot 1)+(3\cdot 4)\=2+12=14\end{aligned}}.
使用交叉积
交叉积是另一种向量相乘的方法。它产生另一个向量。使用分量形式。
a × b = | a | b | sin ( θ ) n {displaystyle /mathbf {a} /times /mathbf {b} =|/mathbf {a} =|/mathbf {b} =||mathbf {b}|mathbf {b}|sin(theta )/mathbf {n}。}
这里 | a | {displaystyle |mathbf {a} {displaystyle |mathbf {a}}指的是 {displaystyle {mathbf {a}}的长度。|}




乘以一个标量
要用一个标量(一个正常的数字)乘以一个向量,你要用这个数字乘以向量的每个分量。
c x = ( c x , 1c x ,2 . . , c x n ) {\displaystyle c\,\mathbf {x} =(c,x_{1},c,x_{2},...,c,x_{n}) }
这方面的一个例子是
c = x5 = ( , 3)4 c x = ( 5⋅ ,3 5⋅ ) 4= ( ,15 ) {\20displaystyle {begin{aligned}c=5\\mathbf {x} =(3,4)\c,\mathbf {x} =(5\cdot 3,5\cdot 4)\=(15,20)end{aligned})
相关页面
- 矢量图形
- 矢量场
问题和答案
问:什么是矢量?答:矢量是一种数学对象,它有一个大小,称为量值,还有一个方向。它通常用黑体字或从一点到另一点的线段表示。
问:我们通常如何画矢量?
答:我们通常把向量画成箭头。箭头的长度与向量的大小成正比,箭头指向的方向就是向量的方向。
问:有人问路是什么意思?
答:问路时,如果说 "朝北走一公里",那就是矢量,但如果说 "走一公里",不表明方向,那就是标量。
问:有哪些关于如何使用向量的例子?
答:向量可以用来显示事物移动的距离和方向。它们也可以在问路或导航时使用。
问:向量在数学上是如何表示的?
答:向量通常用黑体字表示(如u、v、w),或用从一点到另一点的线段表示(如A→B)。
问:当某物被称为标量时是什么意思?
答:当某物被称为标量时,意味着没有任何与之相关的方向性信息,只有距离或速度等数值。
搜索百科全书











