初等代數
初级代数是教给学生的最基本的代数形式。它往往是继算术之后,下一个教给学生的数学领域之一。在算术中,只有数字和运算符如+、-、×、÷出现;而在代数中,变量(如a、x、y)被用来代表数字。这一点很有用,因为。
- 它让人们解决关于"未知"数字的问题。这意味着学习方程和如何解决它们(例如,"找到一个数字x,其中3 x + 1 = 10 {\displaystyle 3x+1=10
}")。
- 它可以从算术中概括出规则。虽然有的学生明白3+4=4+3 {/displaystyle 3+4=4+3}。
这使得代数成为学习抽象的良好步骤(从许多例子中学习一般的想法)。
- 它可以帮助人们理解和创建功能关系(有时也称为因果关系)。一个例子是"如果卖出x张票,那么利润将是3×-10 {\displaystyle 3x-10}
美元"。
这三个是初级代数的主要支线。初级代数在很多其他科目中也经常用到,比如理科、商科、建筑。抽象代数,是一个更高级的课题,一般在大学后期才教。
简单代数问题
如果一个方程只有一个未知数,有时很容易解。这个未知数叫做"x"。
2 x + 4 = 12.{displaystyle 2x+4=12.}。
要解一个有一个未知数的简单方程,要把方程的两边加、减、乘或除以相同的数,以便把未知数x放在方程的一边。一旦x被自己放在一边,就用算术来确定等式另一边的量。例如,从上式中的两边减去4。
2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4=12-4,}。
越来越。
2 x = 8 {\displaystyle 2x=8,\}。
两边除以2。
2 x 2 = 8 2 {displaystyle {frac {2x}{2}}={frac {8}{2}}}},}。
越来越。
x = 4.{displaystyle x=4.\,}。
把这个等式看成是一个跷跷板或平衡,你对一边做什么,你就必须对另一边做什么,你的主要目的是自己得到x。
定义
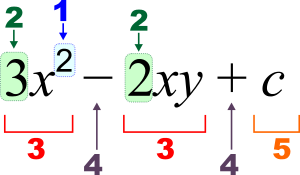
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c
1:指数(幂),2:系数,3:项,4:算子,5:常数,x、y {\displaystyle x,y}
问题和答案
问:什么是初等代数?答:初等代数是教给学生的最基本形式的代数。它通常是在算术之后,涉及使用变量(如a、x、y)来代表方程中的数字。
问:初等代数有哪些用途?
答:初等代数可用于解决有关未知数的问题,从算术中归纳出规则,理解和建立函数关系,并经常用于许多其他学科,如科学、商业和建筑。
问:初等代数是如何帮助人们理解抽象概念的?
答:初等代数通过证明a+b=b+a适用于所有a和b的情况,帮助人们从许多例子中学习一般概念,这使他们能够更好地理解抽象概念。
问:抽象代数是否比初等代数更高级?
答:是的,抽象代数一般在大学后期教授,比初等代数要高级得多。
问:初等代数涉及哪些类型的方程?
答:初等代数涉及到方程,变量(如a,x,y)代表数字,以及运算符如+,-,×,和÷。
3x+1=10 {displaystyle 3x+1=10}。
问:理解初等代数对其他科目有什么帮助?
答:理解初等代数可以帮助其他学科,如科学、商业或建筑,因为它可以让人们解决有关未知数的问题,并在不同变量之间建立函数关系。
搜索百科全书




