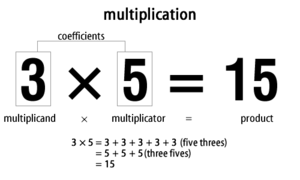
乘法
乘法是求两个数的乘积的一种算术运算。乘法是数学中继加法之后的第三种运算,加法是第一种,减法是第二种,然后是乘法。
用自然数,它可以告诉你一个长方形中,两个数中的一个数等于一边的瓦片数,另一个数等于另一边的瓦片数。
对于实数,它告诉你一个长方形的面积,其中第一个数字等于一条边的大小,第二个数字等于另一条边的大小。
例如,3乘以5,就是5个3相加的总和,或3个5的总和。这可以写成3×5=15,也可以说成"3乘以5等于15"。数学家把你要乘的两个数一起叫做"系数",或者分别叫做"乘方"和"乘器"。乘数×乘数=乘积。
数字之间的乘法被认为是互换的--当数字的顺序不影响乘积的值时。这对于整数(整数)来说是正确的,例如4×6和6×4是一样的,对于有理数(分数)来说也是正确的,对于所有其他实数(可表示为连续线上的域)来说也是正确的,对于复数(可表示为平面上的域)来说也是正确的。但对于四元数(可在四维空间中用环表示的数)、向量或矩阵则不适用。
将乘法定义为重复的加法,提供了一种方法,可以得出对基数乘法的集合论解释。更准确的表达方式是将其视为缩放量。这个动画展示了3乘以2,结果是6。请注意,长度为 3 的蓝色线段中的蓝色小点位于 1 的位置,蓝色线段经过缩放后,这个小点位于长度为 2 的红色线段的末端。对于任何 X 的乘法,蓝色小点总是以 1 为起点,以 X 为终点。
乘法的对面是除法。
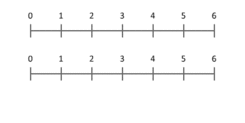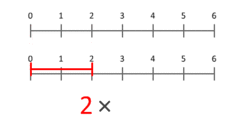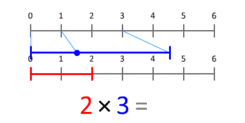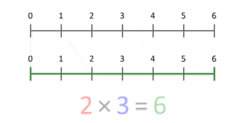

乘法表
教师在教学乘法时,通常要求学生记住前9个数的表。
| 表6 |
| 乘法表 |
| 表1 | | 1 | × | 0 | = | 0 | | 1 | × | 1 | = | 1 | | 1 | × | 2 | = | 2 | | 1 | × | 3 | = | 3 | | 1 | × | 4 | = | 4 | | 1 | × | 5 | = | 5 | | 1 | × | 6 | = | 6 | | 1 | × | 7 | = | 7 | | 1 | × | 8 | = | 8 | | 1 | × | 9 | = | 9 | | 1 | × | 10 | = | 10 | | | 表2 | | 2 | × | 0 | = | 0 | | 2 | × | 1 | = | 2 | | 2 | × | 2 | = | 4 | | 2 | × | 3 | = | 6 | | 2 | × | 4 | = | 8 | | 2 | × | 5 | = | 10 | | 2 | × | 6 | = | 12 | | 2 | × | 7 | = | 14 | | 2 | × | 8 | = | 16 | | 2 | × | 9 | = | 18 | | 2 | × | 10 | = | 20 | | | 表3 | | 3 | × | 0 | = | 0 | | 3 | × | 1 | = | 3 | | 3 | × | 2 | = | 6 | | 3 | × | 3 | = | 9 | | 3 | × | 4 | = | 12 | | 3 | × | 5 | = | 15 | | 3 | × | 6 | = | 18 | | 3 | × | 7 | = | 21 | | 3 | × | 8 | = | 24 | | 3 | × | 9 | = | 27 | | 3 | × | 10 | = | 30 | | | 表4 | | 4 | × | 0 | = | 0 | | 4 | × | 1 | = | 4 | | 4 | × | 2 | = | 8 | | 4 | × | 3 | = | 12 | | 4 | × | 4 | = | 16 | | 4 | × | 5 | = | 20 | | 4 | × | 6 | = | 24 | | 4 | × | 7 | = | 28 | | 4 | × | 8 | = | 32 | | 4 | × | 9 | = | 36 | | 4 | × | 10 | = | 40 | | | 表5 | | 5 | × | 0 | = | 0 | | 5 | × | 1 | = | 5 | | 5 | × | 2 | = | 10 | | 5 | × | 3 | = | 15 | | 5 | × | 4 | = | 20 | | 5 | × | 5 | = | 25 | | 5 | × | 6 | = | 30 | | 5 | × | 7 | = | 35 | | 5 | × | 8 | = | 40 | | 5 | × | 9 | = | 45 | | 5 | × | 10 | = | 50 | |
| 6 | × | 0 | = | 0 | | 6 | × | 1 | = | 6 | | 6 | × | 2 | = | 12 | | 6 | × | 3 | = | 18 | | 6 | × | 4 | = | 24 | | 6 | × | 5 | = | 30 | | 6 | × | 6 | = | 36 | | 6 | × | 7 | = | 42 | | 6 | × | 8 | = | 48 | | 6 | × | 9 | = | 54 | | 6 | × | 10 | = | 60 | | | 表7 | | 7 | × | 0 | = | 0 | | 7 | × | 1 | = | 7 | | 7 | × | 2 | = | 14 | | 7 | × | 3 | = | 21 | | 7 | × | 4 | = | 28 | | 7 | × | 5 | = | 35 | | 7 | × | 6 | = | 42 | | 7 | × | 7 | = | 49 | | 7 | × | 8 | = | 56 | | 7 | × | 9 | = | 63 | | 7 | × | 10 | = | 70 | | | 表8 | | 8 | × | 0 | = | 0 | | 8 | × | 1 | = | 8 | | 8 | × | 2 | = | 16 | | 8 | × | 3 | = | 24 | | 8 | × | 4 | = | 32 | | 8 | × | 5 | = | 40 | | 8 | × | 6 | = | 48 | | 8 | × | 7 | = | 56 | | 8 | × | 8 | = | 64 | | 8 | × | 9 | = | 72 | | 8 | × | 10 | = | 80 | | | 表9 | | 9 | × | 0 | = | 0 | | 9 | × | 1 | = | 9 | | 9 | × | 2 | = | 18 | | 9 | × | 3 | = | 27 | | 9 | × | 4 | = | 36 | | 9 | × | 5 | = | 45 | | 9 | × | 6 | = | 54 | | 9 | × | 7 | = | 63 | | 9 | × | 8 | = | 72 | | 9 | × | 9 | = | 81 | | 9 | × | 10 | = | 90 | | | 表10 | | 10 | × | 0 | = | 0 | | 10 | × | 1 | = | 10 | | 10 | × | 2 | = | 20 | | 10 | × | 3 | = | 30 | | 10 | × | 4 | = | 40 | | 10 | × | 5 | = | 50 | | 10 | × | 6 | = | 60 | | 10 | × | 7 | = | 70 | | 10 | × | 8 | = | 80 | | 10 | × | 9 | = | 90 | | 10 | × | 10 | = | 100 | |
| | | | | | |
问题和答案
问:什么是乘法?
答:乘法是一种算术运算,用于寻找数学中两个数字的乘积。它通常用×和⋅等符号表示。
问:要相乘的两个数字叫什么?
答:被乘的两个数被称为 "系数",或分别称为 "乘方 "和 "被乘方"。
问:乘法是换元的吗?
答:是的,数字之间的乘法被认为是换元的--当数字的顺序不影响产品的价值时。这对整数、有理数、实数和复数都是如此。然而,对于四元数、向量或矩阵来说,这不是真的。
问:我们如何解释心数的乘法?
答:我们可以把心数的乘法解释为比例量--当一个数字(乘方)被比例化后,放在位置1的点最终会在某个点(乘方)。
问:如何表示3乘以5?
答:3乘以5可以写成3×5=15,或者讲成 "3乘以5等于15"。
问:什么是乘法的反义词?
答:乘法的反义词是除法。
搜索百科全书