代数
代数(来自阿拉伯语:اجبر,译为"al-jabr",意为"破碎部分的重聚")是数学的一部分(在美国通常称为数学,在英国称为数学或算术)。它用变量来表示一个尚未知道的值。当使用等号(=)时,称为方程。一个非常简单的使用变量的方程是:2+3=x。在这个例子中,x=5,或者也可以说"x等于5"。这就叫求x的解。
除了方程,还有不等式(小于和大于)。一种特殊类型的方程叫做函数。它经常被用于制作图形,因为它总是将一个输入转化为一个输出。
代数可以用来解决实际问题,因为代数的规则在现实生活中起作用,数字可以用来表示实际事物的价值。物理、工程和计算机编程是经常使用代数的领域。代数在测量、建筑和商业,特别是会计方面也很有用。
做代数的人都会用到数字的规则和用于数字的数学运算。最简单的是加、减、乘、除。更高级的运算涉及指数,从平方和平方根开始。
代数最初是用来解方程和不等式的。两个例子是线性方程(直线的方程,y=mx+b)和二次方程,二次方程的变量是平方的(与自己相乘,例如:2*2,3*3,或x*x)。
历程
早期的代数形式是由巴比伦人和希腊几何学家(如亚历山大的赫萝)发展起来的。然而,"代数"一词是阿拉伯语Al-Jabr("铸造")的拉丁文形式,来自一本数学书Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah("关于铸造和方程计算的论文"),由波斯数学家Muhammad ibn Mūsā al-Khwārizmī写于9世纪,他是生于乌兹别克斯坦Khwarizm的穆斯林。他在伊拉克巴格达的Al-Ma'moun领导下一直到公元813-833年都很兴盛,约在公元840年去世。该书在12世纪被带到欧洲,并被翻译成拉丁文。该书于是被冠以"代数"之名。数学家名字的结尾al-Khwarizmi被改成了拉丁文中比较容易说的一个词,成为英文的算法)。
例子
下面是一个简单的代数问题的例子。
苏有12颗糖,安有24颗糖。他们决定分享,这样他们就有同样数量的糖果。每人有多少糖果?
这些都是你可以用来解决问题的步骤。
- 为了得到相同数量的糖果,Ann必须给Sue一些。让x代表安给苏的糖果数量。
- 苏的糖果加x,一定和安的糖果减x一样,写成。12 + x = 24 - x
- 从等式的两边减去12,得到:x=12-x。这样就得到:x = 12 - x。(等号一边发生的事情也必须发生在另一边,这样等式才仍然是真的。所以在这种情况下,当12从两边减去时,有一个中间步骤是12+x-12=24-x-12。当一个人自如地掌握了这一点后,中间步骤就不写了)。
- 将x加到等式的两边。由此可得:2x=12
- 将等式两边都除以2,则x=6。答案是6。如果Ann给Sue 6颗糖果,那么她们的糖果数量是一样的。
- 为了检查这一点,将6放回原方程中x所在的位置:12+6=24-6。
- 这就得出18=18,这是真的。他们现在每人都有18颗糖果。
通过练习,当面临一个太难解决的问题时,代数可以被用来解决其他方法。诸如修建一条高速公路、设计一部手机、或找到一种疾病的治疗方法等问题都需要用到代数。
写代数
减去z从y(或y减z)写为y - z.除以z(或y过z:y z {\displaystyle y \over z}
在代数中,将y乘以z(或y乘以z)可以有4种写法:y×z、y*z、y-z或只写yz。通常不用乘法符号"×",因为它看起来太像字母x,而x经常被用作变量。另外,当乘一个较大的表达式时,可以使用括号:y(z+1)。
在代数中,当我们把一个数字和一个字母相乘时,我们把数字写在字母前面。5×y=5y。当数字是1时,则不写1,因为1乘以任何数都是这个数(1×y=y),所以不需要写。
顺便说一下,在代数中,你不一定要用字母x或y。变量只是表示一些未知数或数值的符号,所以你可以使用任何变量。
函数和图形
代数的一个重要部分是研究函数,因为函数经常出现在我们要解决的方程中。函数就像一台机器,你可以把一个或多个数字放入其中,然后得到一个或多个数字。在使用函数时,图形可以成为帮助我们研究方程解的有力工具。
图形是显示使等式或不等式为真的所有变量值的图片。通常当只有一个或两个变量时,这很容易做出。图形通常是一条线,如果这条线不弯曲或不直上直下,它可以用基本公式y=mx+b来描述,变量b是图形的y截距(线与纵轴交叉的地方),m是线的斜率或陡度。这个公式适用于图形的坐标,线上的每一点都写为(x,y)。
在一些数学问题中,比如一条线的方程,可以有多个变量(这里是x和y)。为了找到线段上的点,需要改变一个变量。被改变的变量叫做"独立"变量。然后再进行数学运算,做出一个数。做出来的数字叫做"因变量"。大多数情况下,自变量写成x,因变量写成y,例如,在y=3x+1。这通常放在图形上,使用x轴(向左和向右)和y轴(向上和向下)。它也可以用函数形式写成:f(x) = 3x + 1。所以在这个例子中,我们可以将x填入5,得到y=16。在x上填入2,得到y=7。在x上填入0,得到y=1。所以有一条线穿过(5,16)、(2,7)和(0,1)这三点,如右图所示。
如果x的幂是1,它是一条直线。如果它是平方或其他的幂,它将是一条曲线。如果它使用了不等式(<或>),那么通常图形的一部分会在线的上方或下方有阴影。
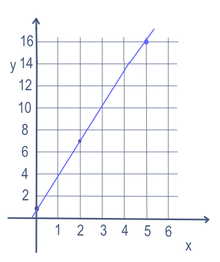
y=3x+1的线性方程。
代数规则
在代数中,有一些规则可以用来进一步理解方程。这些规则被称为代数的规则。虽然这些规则看起来似乎毫无意义或显而易见,但明智的做法是了解这些特性并不是在数学的所有分支中都成立。因此,在认为这些公理规则是理所当然的之前,先了解一下这些公理规则是如何声明的,将是很有用的。在继续讨论这些规则之前,先思考一下将要给出的两个定义。
- Opposite - a {/displaystyle a
}的反面是 - a {/displaystyle -a
}。
- 互惠 - 一个{displaystyle a
}的互惠是1 a {displaystyle {frac {1}{a}}}}。
.
规则
加法的交换性
'换算'是指一个函数如果把数字换来换去,结果是一样的。换句话说,方程中各项的顺序并不重要。当两个项的运算符是加法时,'加法的共通性'是适用的。在代数术语中,这给出了a + b = b + a {\displaystyle a+b=b+a
请注意,这不适用于减法!(即a - b ≠ b - a {\displaystyle a-b\neq b-a})。(即a - b ≠ b - a {\displaystyle a-b\neq b-a
乘法的共轭性
当两个项的运算符是乘法时,"乘法的互换性质"是适用的。用代数术语来说,这就给出了a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a}
注意,这不适用于除法!(即a b≠b a {\displaystyle {\frac {a}{b}}/neq {\frac {b}{a}}}}。

加法的关联性
'联想'指的是数字的分组。加法的联想属性意味着,当把三个或更多项相加时,这些项如何分组并不重要。Algebraically, this gives a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} 

乘法的关联性
乘法的关联性意味着,当三个或更多项相乘时,这些项如何分组并不重要。代数上,这给出了a⋅ ( b⋅ c ) = ( a⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)cdot c}

分配财产
分布属性指出,一个数与另一个项相乘可以进行分布。例如:a⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac

加法身份属性
'身份'是指一个数的属性,即它与自己相等。换句话说,存在着对两个数的运算,使它等于和的变量。加法身份属性指出,任何数字和0的和都是这个数字:a + 0 = a {\displaystyle a+0=a

乘法特性
乘法特性说明任何数和1的乘积都是这个数:a ⋅ 1 = a {\displaystyle a\cdot 1=a

加法逆属性
加法反性质有点像加法特性的反面。当一个运算是一个数和它的相反数之和,并且它等于0时,这个运算就是一个有效的代数运算。在代数上,它声明如下:a - a = 0 {\displaystyle a-a=0
乘法逆属性
乘法反性质意味着,当一个运算是一个数和它的倒数的乘积,并且它等于1时,这个运算是一个有效的代数运算。在代数上,它规定如下: a a = 1 {\displaystyle {\frac {a}{a}{a}}=1
高级代数
除了"初级代数"或基础代数外,还有一些高级形式的代数,在高校中教授,如抽象代数、线性代数和通用代数。其中包括如何利用矩阵同时求解许多线性方程。抽象代数是研究在方程中发现的事物,超越了数字的范畴,以数组为单位,更加抽象。
许多数学问题都是关于物理学和工程学的。在许多物理问题中,时间是一个变量。使用代数中的基本概念可以帮助将数学问题简化为最简单的形式,使其更容易解决困难的问题。能量是e,力是f,质量是m,加速度是a,光速有时是c。这在一些著名的方程中使用,如f=ma和e=mc^2(尽管最后一个方程需要更复杂的代数以外的数学来得出)。
相关网页
- 数学课题清单
- 行动顺序
- 抛物线
- 计算机代数系统
问题和答案
问:什么是代数?答:代数是数学的一部分,它用变量来表示一个尚不知道的数值。
问:代数中的等号表示什么?
答:等号(=)表示代数中的一个等式。
问:什么是代数中的函数?
答:代数中的函数是一种特殊类型的方程,它总是把一个输入变成一个输出。
问:代数如何用于解决实际问题?
答:代数可以用来解决实际问题,因为代数的规则在现实生活中是可行的,数字可以用来表示实际事物的价值。物理学、工程学和计算机编程是一直在使用代数的领域。在测量、建筑和商业领域,特别是会计领域,了解代数也是很有用的。
问:在代数中,有哪些用于数字的数学运算?
答:在代数中,人们使用数字的规则和数学运算,如数字的加、减、乘、除。更高级的运算涉及指数,从平方和平方根开始。
问:代数中使用的方程的例子是什么?
答:代数中使用的方程例子包括线性方程(直线的方程)和二次方程,二次方程的变量是平方(乘以自身)。
搜索百科全书