量子力学
量子力学或QM,描述了宇宙如何在比原子更小的层面上工作。它也被称为 "量子物理学 "或 "量子理论"。量子在拉丁语中是 "多少 "的意思,而力学是与运动有关的科学领域。一个量子的能量是一个特定数量的能量,而量子力学描述了该能量如何在亚原子水平上运动和互动。
原子曾经被认为是物质的最小构成单位,但现代科学表明,还有更小的粒子,如质子、中子和电子。质量管理是物理学的一部分,它描述了构成原子的粒子如何工作。
量子力学还告诉我们电磁波(如光)如何工作。现代物理学和化学的许多内容都可以用量子力学的数学规则来描述和理解。
用于研究亚原子粒子和电磁波的数学是非常复杂的,因为它们以非常奇怪的方式行动。
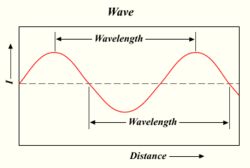
一道光波的波长
波和光子
光子是比原子、质子和电子小得多的粒子;事实上,它们根本就没有任何质量。光子就像能量的 "包 "或包裹。蜡烛或激光器等光源射出(或 "发射")的光是被称为光子的比特。
一盏灯射出的光子越多,光线就越亮。光是一种能量形式,其行为类似于水中的波或无线电波。一个波的顶部和下一个波的顶部之间的距离被称为 "波长"。每个光子都携带一定量的能量,或称 "量子",取决于其波长。
一道光的颜色取决于它的波长。紫色(彩虹的底部或最里面的颜色)的波长约为400纳米("纳米"),相当于0.00004厘米或0.0016英寸。波长为10-400纳米的光子被称为紫外线(或UV)光。这种光不能被人眼看到。在光谱的另一端,红光约为700纳米。红外线约为700纳米至300,000纳米。人眼对红外光也不敏感。
波长并不总是那么小。无线电波的波长更长。调频收音机的波长可以有几米长(例如,在99.5调频上发射的电台发出的无线电能量的波长约为3米,约为10英尺)。每个光子都有一定量的能量,与它的波长有关。一个光子的波长越短,其能量就越大。例如,紫外线光子的能量比红外线光子的能量大。
波长和频率(每秒波峰的次数)是成反比的,这意味着波长越长,频率就越低,反之亦然。如果光的颜色是红外线(频率比红光低),每个光子可以加热它所击中的东西。因此,如果一盏强红外灯(发热灯)对着一个人,这个人就会感到温暖,甚至发热,因为许多光子中储存着能量。红外线灯的表面甚至可能会变热,足以灼伤可能接触到它的人。人类无法看到红外光,但我们可以感受到以热的形式存在的辐射。例如,一个人走过一栋被太阳加热过的砖头建筑,不用触摸就能感受到建筑的热量。
量子力学的数学计算公式是抽象的。一个被称为波函数的数学函数提供了关于粒子的位置、动量和其他物理特性的概率振幅(概率振幅的平方就是概率)的信息。量子力学的许多结果在经典力学方面不容易被直观化。
紫外线的频率比紫光高,因此它甚至不在可见光范围内。紫外线范围内的每个光子都有很大的能量,足以伤害皮肤细胞并导致晒伤。事实上,大多数形式的晒伤不是由热引起的;它们是由太阳的紫外线的高能量损害你的皮肤细胞引起的。甚至更高频率的光(或电磁辐射)可以深入人体,造成更大的损害。X射线的能量非常大,可以深入人体并杀死细胞。人类无法看到或感觉到紫外线或X射线。他们可能只有在被辐射灼伤时才知道自己曾在这种高频率的光线下。对杀死病菌很重要的领域经常使用紫外线灯来消灭细菌、真菌等。X射线有时被用来杀死癌细胞。
量子力学是在发现一定的频率意味着一定量的能量时开始的。能量与频率成正比(E ∝ f)。频率越高,光子的能量就越大,它能造成的损害也就越大。量子力学后来发展到解释原子的内部结构。量子力学还解释了光子可以与自身相互干扰的方式,以及许多其他在经典物理学中从未想象过的事情。
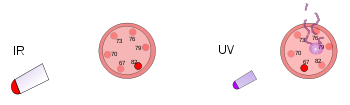
在左边,一个塑料温度计被放在一个明亮的热灯下。这种红外线辐射使温度计变暖,但不会损坏温度计。在右边,另一个塑料温度计受到低强度紫外线的照射。这种辐射会损坏温度计,但不会使其变暖。

左边的黑色是紫外线(高频率);右边的黑色是红外线(低频率)。
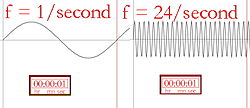
频率的图像描述
量化
马克斯-普朗克发现了频率和能量之间的关系。之前没有人猜到频率与能量是成正比的(这意味着当它们中的一个加倍时,另一个也会加倍)。在所谓的自然单位下,那么代表光子频率的数字也将代表其能量。那么这个方程式就会是。
E = f
意味着能量等于频率。
但从物理学的发展来看,用于测量能量的单位和通常用于测量时间(因此也包括频率)的单位之间没有自然联系。因此,普朗克为使这些数字都正确出来而制定的公式是。
E = h × f
或者,能量等于h乘以频率。这个h是一个以其发现者命名的数字,称为普朗克常数。
量子力学是基于这样的知识:一定频率的光子意味着一定量的能量的光子。除了这种关系,一种特定的原子只能发出某些频率的辐射,所以它也只能发出具有一定能量的光子。
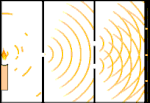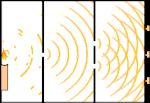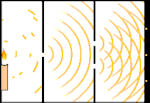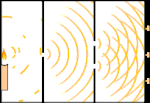
双缝实验:光线从左边的光源到右边的流苏(在黑边上标记)。
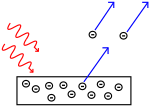
光电效应:光子击中金属,电子被推开。
历史
艾萨克-牛顿认为,光是由非常小的东西组成的,我们现在称之为粒子(他把它们称为 "细胞")。克里斯蒂安-惠更斯(Christiaan Huygens)认为,光是由波组成的。科学家们认为,一个东西不可能同时是一个粒子和一个波。
科学家们做了一些实验来找出光是由粒子还是由波组成的。他们发现两种想法都是对的--光在某种程度上既是波又是粒子。托马斯-杨进行的双缝实验表明,光必须像波一样行动。爱因斯坦发现的光电效应证明,光必须像携带特定数量能量的粒子一样行动,而且能量与它们的频率有关。这一实验结果被称为量子力学中的 "波粒二象性"。后来,物理学家们发现,任何事物的行为都既像波又像粒子,不仅仅是光。然而,这种效应在大型物体中要小得多。
以下是一些发现量子力学基本部分的人。Max Planck, Albert Einstein, Satyendra Nath Bose, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, John von Neumann, and Richard Feynman。他们在20世纪上半叶完成了他们的工作。

从左到右。Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.
超越普朗克
量子力学的公式和观点是为了解释发光的氢气所发出的光。原子的量子理论还必须解释为什么电子会停留在它的轨道上,而其他观点却无法解释。从以前的观点来看,电子必须落到原子的中心,因为它一开始就被自己的能量保持在轨道上,但当它在轨道上旋转时,会很快失去能量。(这是因为电子和其他带电粒子在改变速度或转动时,已知会发出光并失去能量)。
氢气灯的工作原理类似于霓虹灯,但霓虹灯有自己独特的一组颜色(和频率)的光。科学家们了解到,他们可以通过它们产生的光色来识别所有的元素。他们只是无法弄清这些频率是如何确定的。
然后,一位名叫约翰-巴尔默的瑞士数学家想出了一个方程式,告诉人们λ(λ,指波长)会是多少。
λ = B ( n n 22- 4) n = ,3 , 4, {56displaystyle\lambda =B\left({frac {n^{2}}{n^{2}-4}}\right)\qquad n=3, 4, 5, 6}.
其中B是巴尔默确定的一个数字,等于364.56纳米。
这个方程式只对氢气灯发出的可见光有效。但后来,这个方程被变得更加普遍。
1λ = R ( m12 -1 n ) 2,{\displaystyle {frac {1}{lambda }}=R\left({frac {1}{m^{2}}}-{frac {1}{n^{2}}}}right),}。
其中R是Rydberg常数,等于0.0110纳米−1,而且n必须大于m。
为m和n输入不同的数字,很容易预测许多类型的光(紫外线、可见光和红外线)的频率。要看这是如何工作的,请到超级物理学,并在页面的中间往下看。(用H=1表示氢气)。
1908年,沃尔特-里茨提出了里茨组合原理,表明频率之间的某些间隙是如何不断重复的。几年后,这对维尔纳-海森堡来说是很重要的。
1905年,爱因斯坦利用普朗克的想法表明,一束光是由称为光子的粒子流组成的。每个光子的能量取决于其频率。爱因斯坦的想法是量子力学思想的开端,即所有的亚原子粒子,如电子、质子、中子和其他粒子,同时是波和粒子。(见原子的图片,电子是原子的波。)这导致了一个关于亚原子粒子和电磁波的理论,称为波粒二象性。这就是粒子和波既不是一个也不是另一个,而是具有两者的某些属性。
1913年,尼尔斯-玻尔提出了一个想法,即电子只能占用原子核周围的某些轨道。根据玻尔的理论,上面的方程式中称为m和n的数字可以代表轨道。玻尔的理论说,电子可以开始在一些轨道m和结束在一些轨道n,或电子可以开始在一些轨道n和结束在一些轨道m,所以如果一个光子击中一个电子,其能量将被吸收,电子将移动到一个更高的轨道,因为该额外的能量。根据玻尔的理论,如果一个电子从较高的轨道落到较低的轨道上,那么它将不得不以光子的形式放弃能量。光子的能量将等于两个轨道之间的能量差,而光子的能量使它具有一定的频率和颜色。玻尔的理论对亚原子现象的许多方面提供了很好的解释,但未能回答为什么发光的氢(以及发光的氖或任何其他元素)产生的每种颜色的光都有自己的亮度,而且每种元素的亮度差异总是相同。
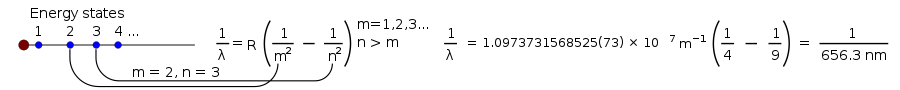
当尼尔斯-玻尔提出他的理论时,关于氢气灯所产生的光的大部分事情都已经知道了,但科学家们仍然无法解释发光的氢气所产生的每条线的亮度。
Werner Heisenberg承担了解释每条线的亮度或 "强度 "的工作。他不能使用任何像巴尔默想出的那种简单的规则。他不得不使用非常困难的经典物理学数学,该数学以电子的质量(重量)、电子的电荷(静态电强度)和其他微小数量来计算一切。经典物理学已经对氢气灯产生的色带的亮度有了答案,但经典理论说,应该有一个连续的彩虹,而不是四个独立的色带。海森堡的解释是。
有一些定律说,发光的氢气会产生什么频率的光。它必须预测当有关电子在靠近原子核(中心)的轨道之间移动时的间隔频率,但它也必须预测,当我们看电子在轨道之间移动的时候,频率会越来越近,越来越远的频率。它还会预测,当我们出去时,频率之间的强度差异会越来越近。经典物理学已经通过一组方程给出了正确的答案,而新物理学必须通过不同的方程给出同样的答案。
经典物理学使用法国数学家傅里叶的方法来对物理世界进行数学描绘,它使用平滑曲线的集合,这些曲线一起构成一条平滑曲线,在这种情况下,从一些光线中给出所有频率的光的强度。但这是不对的,因为那条平滑曲线只出现在较高的频率上。在较低的频率下,总是有一些孤立的点,没有任何东西把这些点连接起来。因此,为了制作一个真实世界的地图,海森堡不得不做出一个重大改变。他必须做一些事情,只挑选出与自然界中所看到的相匹配的数字。有时人们说他 "猜测 "了这些方程式,但他不是在盲目猜测。他找到了他需要的东西。他计算出来的数字会在图表上画出一些点,但在这些点之间没有画线。为每一组计算做一个只有点的 "图 "会浪费很多纸,而且什么也做不了。海森堡找到了一种方法来有效地预测不同频率的强度,并以一种有用的方式组织这些信息。
仅仅使用上面给出的经验法则,即巴尔默开始的和赖德伯格改进的法则,我们就可以看到如何得到一组数字,以帮助海森堡得到他想要的那种画面。
这个规则说,当电子从一个轨道移动到另一个轨道时,它要么获得能量,要么失去能量,取决于它是离中心越来越远还是越来越近。因此,我们可以把这些轨道或能级作为标题沿着网格的顶部和侧面放进去。由于历史原因,最低的轨道被称为n,而接下来的轨道被称为n-a,然后是n-b,以此类推。令人困惑的是,当电子实际上在获得能量时,他们使用了负数,但这就是它的方式。
由于赖德伯格规则给我们提供了频率,我们可以根据电子的去向,用这个规则来输入数字。如果电子从n处开始,最后停留在n处,那么它就没有真正去任何地方,所以它没有获得能量,也没有失去能量。如果电子从n-a开始,最后在n结束,那么它就从一个较高的轨道落到一个较低的轨道。如果它这样做了,那么它就失去了能量,而它失去的能量就表现为一个光子。光子有一定的能量,e,这与一定的频率f有关,公式为e=h f。所以我们知道,一定的轨道变化会产生一定频率的光,f。只有当一个具有一定频率和能量的光子从外面进来,被电子吸收并赋予其能量时,才会发生这种情况,而这正是使电子走到更高轨道的原因。因此,为了使一切都有意义,我们把这个频率写成一个负数。以前有一个具有一定频率的光子,现在它已经被拿走了。
所以我们可以做一个这样的网格,其中f(a←b)表示电子从能量状态(轨道)b到能量状态a时涉及的频率(同样,序列看起来是倒过来的,但这是它们最初的写法)。
f的网格
| 电子状态 | n | n-a | n-b | n-c | .... | |
| f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | ||
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| n-b | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| 过渡.... | ..... | ..... | ..... | ..... |
海森堡并没有制作这样的网格。他只是做了能让他得到他所寻找的强度的数学运算。但要做到这一点,他必须将两个振幅(一个波的测量高度)相乘来计算强度。(在经典物理学中,强度等于振幅的平方。)他做了一个看起来很奇怪的方程来处理这个问题,写出了他的论文的其余部分,把它交给了他的老板,然后去度假了。博恩博士看着他那有趣的方程式,似乎有点疯狂。他一定在想:"为什么海森堡要给我这个奇怪的东西?为什么他要这样做呢?"然后他意识到,他在看一个他已经非常熟悉的东西的蓝图。他习惯于把我们通过做例如频率的所有数学运算而写出的网格或表格称为矩阵。而海森堡的怪异方程是一个将两个矩阵相乘的规则。马克斯-博恩是一个非常、非常好的数学家。他知道,由于被乘的两个矩阵(网格)代表不同的东西(例如位置(x,y,z)和动量(mv)),那么当你用第一个矩阵乘以第二个矩阵时,你会得到一个答案,当你用第二个矩阵乘以第一个矩阵时,你会得到另一个答案。尽管海森堡并不了解矩阵数学,但他已经看到了这个 "不同答案 "的问题,而且这个问题一直困扰着他。但博恩博士是一位优秀的数学家,他看到第一个矩阵乘法和第二个矩阵乘法之间的差异总是涉及普朗克常数h,乘以负1的平方根i。海森堡所说的 "不确定 "是指像电子这样的东西在被钉住之前是不会被钉住的。它有点像一只水母,总是到处乱挤,除非你杀了它,否则不能 "在一个地方"。后来,人们习惯于把它称为 "海森堡不确定性原理",这使许多人犯了一个错误,认为电子和类似的东西真的 "在某个地方",但我们只是在自己的头脑中不确定。这种想法是错误的。这不是海森堡所谈论的内容。难以测量的东西是一个问题,但它不是海森堡所说的问题。
海森堡的想法非常难以掌握,但我们可以通过一个例子使其更加清晰。首先,我们将开始把这些网格称为 "矩阵",因为我们很快就会需要谈论矩阵乘法。
假设我们从两种测量开始,位置(q)和动量(p)。在1925年,海森堡写了一个类似这样的方程。
Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\displaystyle Y(n,n-b)=\sum _{a}^{}\,p(n,n-a)q(n-a,n-b)}。
他并不知道,但这个方程给出了一个写出两个矩阵(网格)并将其相乘的蓝图。一个矩阵与另一个矩阵相乘的规则有点混乱,但这里是根据蓝图写出的两个矩阵,然后是它们的积。
p的矩阵
| 电子状态 | n-a | n-b | n-c | .... | |
| p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | ||
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| n-b | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| 过渡.... | ..... | ..... | ..... | ..... |
q的矩阵
| 电子状态 | n-b | n-c | n-d | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| n-b | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| 过渡.... | ..... | ..... | ..... | ..... |
海森堡1925年论文中的相关方程所规定的上述两个矩阵的乘积的矩阵是。
| 电子状态 | n-b | n-c | n-d | ..... |
| A | ..... | ..... | ..... | |
| n-a | ..... | B | ..... | ..... |
| n-b | ..... | ..... | C | ..... |
在哪里?
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+.....
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+.....
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+.....
等等。
如果矩阵颠倒过来,将产生以下数值。
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b)+.....
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c)+.....
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+.....
等等。
请注意改变乘法的顺序是如何一步一步地改变实际被乘的数字的。
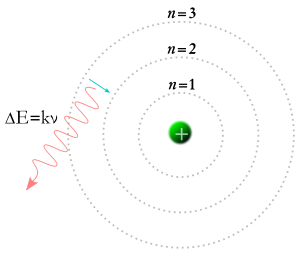
一个电子落到较低的轨道上,一个光子就产生了。
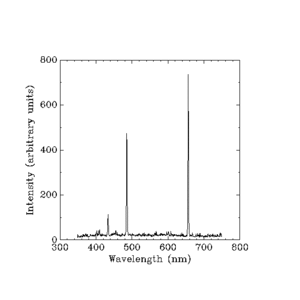
任意单位的间隔强度

发光的氢气所发出的可见光。(波长为纳米)。
超越海森堡
维尔纳-海森堡的工作似乎打破了一个僵局。很快,路易斯-德-布罗格利、马克斯-伯恩、保罗-狄拉克、沃尔夫冈-保利和埃尔温-薛定谔等人提出了许多其他解释事物的不同方法。这些物理学家中的每一位的工作都是自己的故事。海森堡和早期的人所使用的数学并不难理解,但随着物理学家对原子世界的深入研究,这些方程式很快就变得非常复杂。
更多谜团
在量子力学的早期,阿尔伯特-爱因斯坦提出,如果它是正确的,那么量子力学将意味着会有 "远距离的幽灵行动"。事实证明,量子力学是正确的,爱因斯坦用来作为拒绝量子力学的理由的事情确实发生了。某些量子事件之间的这种 "幽灵般的联系 "现在被称为 "量子纠缠"。
当一个实验把两个东西(光子、电子等)聚集在一起时,它们就必须在量子力学中共享一个共同的描述。当它们后来被分开时,它们保持相同的量子力学描述或 "状态"。在图中,一个特性(例如,"上 "自旋)被画成红色,而它的配偶(例如,"下 "自旋)被画成蓝色。紫色的带子意味着,当例如两个电子放在一起时,这对电子同时具有两种特性。因此,两个电子可以显示出上旋或下旋。当它们后来被分开时,一个留在地球上,一个去了半人马座阿尔法星的某个星球,它们仍然各自具有两种自旋。换句话说,它们中的每一个都可以 "决定 "将自己显示为一个自旋向上的电子或一个自旋向下的电子。但如果后来有人测量另一个,它必须 "决定 "显示自己具有相反的自旋。
爱因斯坦认为,在如此遥远的距离上,认为强迫一个电子显示其自旋,然后以某种方式使另一个电子显示出相反的特性是疯狂的。他说,这两个电子肯定一直是自旋向上或自旋向下的,但量子力学无法预测每个电子的特性。无法预测,只能通过正确的实验来观察其中一个,这意味着量子力学无法解释一些重要的东西。因此,爱因斯坦说,量子力学有一个大洞。量子力学是不完整的。
后来,事实证明,实验表明,是爱因斯坦错了。
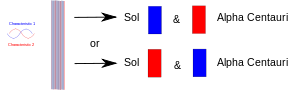
两个纠缠的粒子被分开:一个在地球上,一个被带到某个遥远的星球。测量其中一个,迫使它 "决定 "扮演哪个角色,而另一个在被测量时必须扮演另一个角色(之后)。
海森堡不确定性原理
1925年,维尔纳-海森堡描述了不确定性原理,它说我们对一个粒子的位置知道得越多,我们对它的速度和方向知道得越少。换句话说,我们对小东西的速度和方向了解得越多,对它的位置就越不了解。物理学家在这种讨论中通常会谈论动量,而不是谈论速度。动量只是某物在某个方向上的速度乘以其质量。
海森堡的不确定性原理背后的原因是,我们永远无法同时知道一个粒子的位置和动量。因为光是一种丰富的粒子,它被用来测量其他粒子。测量它的唯一方法是将光波反弹到粒子上并记录结果。如果使用高能量,或高频率的光束,我们可以准确地知道它在哪里,但不能知道它的速度有多快。这是因为高能量的光子将能量转移到粒子上,并改变了粒子的速度。如果我们使用低能量的光子,我们可以知道它的速度有多快,但不能知道它在哪里。这是因为我们使用的是波长较长的光。较长的波长意味着粒子可能在波段的任何地方。
该原则还说,有许多测量对,无论我们如何努力,都不能同时知道任何粒子(一个非常小的东西)的情况。我们对这样的一对中的一个了解得越多,我们对另一个的了解就越少。
即使是阿尔伯特-爱因斯坦也难以接受这样一个奇怪的概念,他在一次著名的辩论中说:"上帝不玩骰子"。对此,丹麦物理学家尼尔斯-玻尔作出了著名的回应:"爱因斯坦,不要告诉上帝该怎么做"。
QM的用途
电子围绕着每个原子的原子核。化学键将原子连接起来,形成分子。当电子在两个原子之间共享时,化学键将两个原子连接起来。因此,QM是化学键的物理学和化学的物理学。QM帮助我们了解分子是如何形成的,以及它们的属性是什么。
QM也可以帮助我们理解大的事物,如恒星,甚至整个宇宙。QM是宇宙如何开始的理论的一个非常重要的部分,称为大爆炸。
一切由物质构成的东西都会被其他物质吸引,因为有一种基本的力量叫做引力。爱因斯坦解释引力的理论被称为广义相对论。现代物理学的一个问题是,QM的一些结论似乎与广义相对论并不一致。
QM是物理学的一部分,它可以解释为什么所有的电子技术都能像这样工作。因此,QM解释了计算机如何工作,因为计算机是电子机器。但1950年或1960年左右的早期计算机硬件的设计者不需要考虑QM。当时的收音机和电视机的设计者也没有想到QM。然而,近年来更强大的集成电路和计算机内存技术的设计确实需要QM。
QM也使诸如以下技术成为可能。
为什么QM难学
QM是一个具有挑战性的课题,有几个原因。
- QM解释事物的方式与我们小时候对世界的了解非常不同。
- 理解QM需要比代数和简单微积分更多的数学知识。它还需要矩阵代数、复数、概率论和偏微分方程。
- 物理学家们不确定QM的一些方程告诉我们现实世界的情况。
- QM表明,原子和亚原子粒子的行为方式很奇怪,完全不像我们在日常生活中看到的那样。
- QM描述的是极其微小的事物,因此,如果没有特殊设备,我们无法看到其中的一些事物,而且我们根本无法看到其中的许多事物。
QM以一种不同于我们通常思考科学的方式来描述自然。它告诉我们一些事情发生的可能性有多大,而不是告诉我们它们肯定会发生。
一个例子是杨氏双缝实验。如果我们从激光器中向一张照相胶片射出单个光子(单个光单位),我们会在冲洗后的胶片上看到一个单个光点。如果我们在中间放一张金属片,并在金属片上开两条很窄的缝,当我们向金属片发射许多光子时,它们必须穿过缝隙,那么我们将看到一些显著的现象。在冲洗过的胶片上,我们将看到一系列的明暗带。我们可以用数学来准确地告诉这些亮带的位置,以及产生这些亮带的光线有多亮,也就是说,我们可以提前知道有多少光子会落在每个亮带上。但如果我们把这个过程放慢,看看每个光子落在屏幕上的位置,我们永远无法提前知道下一个光子会出现在哪里。我们可以确定的是,光子最有可能落在中心的亮带上,而在离中心越来越远的带子上,光子出现的可能性越来越小。因此,我们可以肯定的是,这些带子在中心是最亮的,而在离中心越来越远的地方就会越来越暗淡。但我们永远不知道哪个光子会进入哪个波段。
QM理论的一个奇怪结论是 "薛定谔的猫 "效应。粒子的某些属性,例如它们的位置、运动速度、运动方向和 "自旋",在有东西测量它们之前是谈不上的(例如,从电子上反弹下来的光子将算作对其位置的测量)。在测量之前,粒子处于 "状态的叠加 "中,它的属性同时具有许多数值。薛定谔说,量子力学似乎在说,如果某样东西(比如一只猫的生死)是由量子事件决定的,那么它的状态将由量子事件产生的状态决定,但只是在有人看了量子事件的状态时。在看量子事件的状态之前的时间里,也许 "活猫和死猫(请原谅我的表达)[被]混在一起或被抹去了同等的部分"。
减少的普朗克常数
人们经常使用符号ℏ {displaystyle \hbar } ,这被称为 "h-bar"。

例子
一维井中的粒子是一个最简单的例子,表明粒子的能量只能有特定的值。能量被说成是 "量化 "的。井在某一范围内的势能为零,在该范围外的任何地方都有无限的势能。对于x {displaystyle x}
- 2ℏ2 m d 2ψ d x = 2E ψ 。{displaystyle -{frac {hbar ^{2}}{2m}}{frac {d^{2}psi\}{dx^{2}}=E\psi 。}
使用微分方程,我们可以看到,ψ {displaystyle \psi }
ψ = A e i k x + B e - i k x E = ℏ2 k m {22displaystyle \psi =Ae^{ikx}+Be^{-ikx}\;\;\;\;E={frac {hbar ^{2}k^{2}}{2m}}}。
或
ψ = C sin k x + D cos k x {\displaystyle \psi =C\sin kx+D\cos kx\; }(通过欧拉公式)。
盒子的墙壁意味着波函数必须有一个特殊的形式。在墙壁无限高的任何时候,粒子的波函数必须是零。在每一面墙上
ψ = a 0t x = ,0 x = L {\displaystyle \psi =0\;\mathrm {at}\;\;x=0,\;x=L}。
考虑x = 0
- sin 0 = 0,cos 0 = 1。为了满足ψ={0displaystyle \scriptstyle \psi =0\; }
,cos项必须被删除。因此,D = 0
现在考虑一下。ψ = C sin k x {displaystyle \scriptstyle \psi =C\sin kx\; }
- 在x = L时,ψ = C sin k L = {\0displaystyle \scriptstyle \psi =C\sin kL=0\; }
- 如果C=0,那么ψ={\0displaystyle \scriptstyle \psi =0\; }
对于所有的x,这个解决方案没有用。
- 因此,sin kL = 0一定是真的,我们可以得到
k L = n π n = , 12, 3,4 , 5. . . .{displaystyle kL=npi\;\;\;\;n=1,2,3,4,5,...\; }
我们可以看到,n {displaystyle n}
相关页面
问题和答案
问:什么是量子力学?答:量子力学是物理学的一个分支,解释宇宙如何在比原子更小的范围内运作。它也被称为量子物理学或量子理论。
问:"量子 "这个词是什么意思?
答:"量子 "一词来自拉丁语,意思是 "多少"。一个量子的能量是可能的最小量(或最小的额外量),而量子力学描述了该能量如何移动或相互作用。
问:什么是亚原子粒子?
答:亚原子粒子是构成原子的粒子,如质子、中子和电子。它们甚至比原子还小。
问:量子力学如何描述这些粒子的工作原理?
答:量子力学提供了研究亚原子粒子和电磁波的数学规则,以了解它们的行为和相互之间的相互作用。
问:什么是波粒二象性?
答:波粒二象性是指粒子和波的行为都可以像彼此一样--它们不是两个不同的实体,而是类似于两者结合成一个现象的东西。
问:如何用量子力学来描述现代物理学?
答:现代物理学和化学可以通过运用量子力学的数学规则来解释它们。
搜索百科全书







