皮

近似值

Pi通常被正式写成π或希腊字母π，作为一种快捷方式。Pi也是一个无理数，意味着它不能写成分数( a b {displaystyle a over b} )，其中'a'和'b'是整数（整数）。这基本上意味着，小数点右边的π的数字永远不会重复，而且不可能把π的精确值写成一个数字。圆周率只能是近似值，或测量到一个足以满足实际需要的数值。

一个接近π的数值是3.141592653589793238462643...圆周率的一个常见的分数近似值是22 7 {displaystyle 22\over 7} ，得出约3.14285714。这就产生了大约3.14285714。这个近似值与π的真值相差0.04%。虽然这个近似值在现实生活中的大部分使用是可以接受的，但分数355 113 {displaystyle 355\over 113} 更准确（给出约3.14159292），当需要一个更接近π的值时可以使用。计算机可以用来获得更好的π的近似值。

2019年3月，艾玛-岩尾计算出π的数值为31.4万亿位。

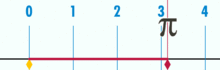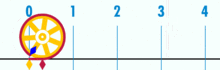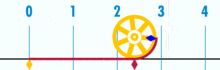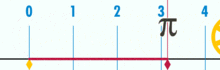
用一个直径为1的圆来表示如何求出π的图示。这个圆的周长是π。

历史

古代印度数学家如Bhaskaracharya和Aryabhatta知道π的数值。

数千年来，数学家们一直知道圆周率，因为他们在同样长的时间里一直在研究圆。像巴比伦人这样古老的文明已经能够将π近似于许多数字，例如分数25/8和256/81。大多数历史学家认为，古埃及人没有π的概念，这种对应关系是一种巧合。

第一个关于圆周率的文字记载可以追溯到公元前1900年。大约在公元前1650年，埃及人阿梅斯在林德纸莎草纸上给出了一个数值。巴比伦人通过简单地做一个大圆，然后在圆周和直径上粘上一根绳子，记下它们的距离，然后用圆周除以直径，就能发现π的值略大于3。

关于圆周率的知识又传到了欧洲，传到了希伯来人的手中，他们在《圣经》中被称为《旧约》的一节中把这个数字列为重要内容。在这之后，试图找到π的最常见的方法是在任何一个圆内画一个多面的形状，用这个形状的面积来求π。例如，希腊哲学家阿基米德用一个有96条边的多边形来寻找π的值，但公元500年的中国人却能用一个有16384条边的多边形来寻找π的值。希腊人，如克拉佐米纳的阿纳克萨戈拉，也忙于找出圆的其他属性，如如何制作圆的正方形和对数字π的平方。从那时起，许多人就一直试图找出更多更精确的π值。

圆周率的历史
哲学家	日期	近似值
克劳迪厄斯-托勒密	公元150年左右	3.1416
祖冲之	430-501 CE	3.1415929203
姆瓦利兹米(al-Khwarizmi)	公元800年左右	3.1416
喀什	1430年左右	3.14159265358979
维埃特	1540-1603	3.141592654
罗敏	1561-1615	3.14159265358979323
范库伦	1600年左右	3.14159265358979323846264338327950288

在16世纪，越来越好的求π方法出现了，比如法国律师François Viète开发的复杂公式。希腊符号 "π "的首次使用是在威廉-琼斯1706年写的一篇文章中。

一位名叫兰伯特的数学家也在1761年表明，数字π是无理的；也就是说，按照正常的标准，它不能被写成分数。另一位名叫林德曼的数学家也在1882年表明，π是被称为超越数的一组数字的一部分，这些数字不能成为多项式方程的解。

除了圆以外，圆周率还可以用来计算许多其他东西。除了研究形状的几何学之外，圆周率的特性使其能够被用于数学的许多其他领域。其中一些领域是复杂分析、三角学和数列。

现实生活中的Pi

今天，有不同的方法来计算π的许多位数，但这用途有限。

Pi有时可以用来计算任何圆的面积或周长。要计算一个圆的周长，可以用公式C（周长）=π乘以直径。要想知道圆的面积，请使用公式π（半径²）。这个公式有时被写成A=π r 2 {\displaystyle A=pi r^{2}} ，其中r是变量，代表圆的面积。其中r是任何圆的半径的变量，A是该圆的面积的变量。

计算一个圆的周长，误差为1毫米。

• 半径为30米时需要4位数字
• 半径等于地球的10位数
• 15位数字，半径等于地球到太阳的距离。

人们一般把3月14日作为圆周率日来庆祝，因为3月14日也被写成3/14，它代表圆周率近似值中的前三个数字3.14。圆周率日始于2001年期间。

相关页面

• 圆圈