普朗克常数

普朗克常数(Planck's constant)将光子携带的能量与它的电磁波频率联系起来。它是以物理学家马克斯-普朗克的名字命名的。它是量子物理学中的一个重要量。

普朗克常数有物理作用的维度：能量乘以时间，或动量乘以距离。在SI单位中，普朗克常数的单位是焦耳秒（J⋅s）或（N⋅m⋅s）或（kg⋅^m2⋅s^-1）。符号的定义如下。

在SI单位中，普朗克常数正好是6.62607015×10^-34 J-s（根据定义）。科学家们用这个量来计算普朗克长度和普朗克时间等测量值。

马克斯・普朗克

柏林洪堡大学前，马克斯-普朗克发现普朗克常数的纪念牌。英文译文："Max Planck, discoverer of the elementary quantum of action h:"马克斯-普朗克，基本量子作用h的发现者，从1889年到1928年在这栋楼里授课。"

背景资料

本文中使用的符号。

符号	意思
E	能源
h	普朗克常数
k	玻尔兹曼常数
c	光速
λ	辐射波长
ν	辐射频率
T	绝对温度

1670年至1900年间，科学家们对光的性质进行了讨论。一些科学家认为，光是由数百万个微小粒子组成的。另一些科学家则认为，光是一种波。

光：波还是粒子？

1678年，克里斯蒂安-惠更斯写了《光论》一书。他认为光是由波组成的。他说，光不可能由粒子组成，因为两束光不会相互反弹。1672年，牛顿写了《光学》一书。他认为光是由红、黄、蓝三色粒子组成的，他把这些粒子称为光团。牛顿用他的"双棱镜实验"来解释这个问题。第一面棱镜将光分解成不同的颜色，第二面棱镜将这些颜色合并。第二面棱镜将这些颜色合并成白光。

在18世纪，牛顿的理论受到了最多的关注。1803年，托马斯-杨描述了"双狭缝实验"。在这个实验中，光通过两个狭窄的缝隙，会对自身产生干扰。这导致了一种模式，表明光是由波组成的。在19世纪余下的时间里，光的波浪理论受到了最多的关注。19世纪60年代，詹姆斯-克拉克-麦克斯韦（James Clerk Maxwell）提出了将电磁辐射描述为波的方程式。

电磁辐射理论把光、无线电波、微波和其他许多类型的波都当作同一种东西，只是它们的波长不同。我们眼睛能看到的光的波长大致在400～600纳米之间。无线电波的波长从10米到1500米不等，微波的波长约为2厘米。在真空中，所有电磁波都以光速传播。电磁波的频率由下列公式给出。

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}}} $\nu ={\frac {c}{\lambda }}$ .

符号在此定义。

黑色车身散热器

所有温暖的东西都会发出热辐射，也就是电磁辐射。对于地球上的大多数事物来说，这种辐射是在红外范围内的，但一些非常热的东西（1000℃以上），会发出可见辐射，也就是光。在19世纪末，许多科学家研究了不同温度下黑体辐射器发出的电磁辐射的波长。

Rayleigh-Jeans Law

1900年，雷利勋爵首次发表了雷利------扬斯定律的基本原理。该理论是基于气体的动力学理论。James Jeans爵士在1905年发表了更完整的理论。该定律将黑体散热器在不同温度下发出的电磁能量的数量和波长联系起来。描述这一情况的方程是：

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={/frac {2ckT}{\lambda ^{4}}}}。 $B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}$ .

对于长波长的辐射，这个方程所预测的结果与在实验室中获得的实际结果很吻合。然而，对于短波长（紫外线），理论与实践之间的差异非常大，因此被称为"紫外线灾难"。

普朗克定律

1895年，维恩发表了他对黑体辐射的研究结果。他的公式是：

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}}。 $B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}$ .

这个公式对短波长的电磁辐射效果很好，但对长波长的电磁辐射效果不好。

1900年，马克斯-普朗克发表了他的研究结果。他试图通过假设辐射由小量子组成，然后看看如果把量子变得无限小，会发生什么情况，开发出用波长表示的黑体辐射的表达式。这是一个标准的数学方法）。其表达式为：

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={frac {2hc^{2}}{\lambda ^{5}}}~{frac {1}{e^{frac {hc}{\lambda kT}}}-1}}}}} $B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}$ .

如果允许光的波长变得非常大，那么可以证明，罗利-吉恩和普朗克关系几乎是相同的。

他计算了h和k，发现

h = 6.55×10^-27 erg-sec.

k = 1.34×10^-16 erg-deg-¹。

其数值分别接近现代公认的6.62606×10^-34和1.38065×10^-16。普朗克定律与实验数据吻合得很好，但它的全部意义在几年后才被人们所认识。

光量子理论

原来，如果光达到一个阈值频率，电子就会被光电效应脱落。低于这个阈值，金属中就不能发出电子。1905年，爱因斯坦发表了一篇论文，解释了这种效应。爱因斯坦提出，一束光不是在空间中传播的波，而是一个离散的波包（光子）的集合，每个波包都有能量。爱因斯坦说，这种效应是由于光子撞击电子所致。这证明了光的粒子性质。

爱因斯坦还发现，波长较长的电磁辐射没有效果。爱因斯坦说，这是因为"粒子"没有足够的能量来干扰电子。

普朗克提出，每个光子的能量与光子频率的关系是普朗克常数。这在数学上可以写成：

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}}} $E=h\nu ={\frac {hc}{\lambda }}$ .

普朗克于1918年获得诺贝尔奖，以表彰他因发现能量量子而对物理学进步所作出的贡献。1921年，爱因斯坦因将普朗克常数与光电效应联系起来而获得诺贝尔奖。

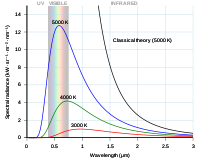
Rayleigh-Jeans曲线和Planck曲线与光子波长的关系图。

索尔韦会议1911年。普朗克、爱因斯坦和詹斯站着。普朗克是第二个从左边。爱因斯坦是第二个从右。詹斯从右边第五位。维恩坐着，右三。

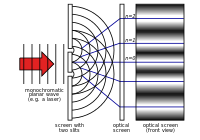
杨氏双缝实验

插图取自牛顿给皇家学会的原信（1671年1月1日[朱利安历]）。S代表太阳光。BC和DE平面之间的光是彩色的。这些颜色在平面GH上重新组合成太阳光。

应用

普朗克常数在许多应用中都很重要。下面列举一些应用。

玻尔原子模型

1913年，尼尔斯-玻尔发表了原子结构的玻尔模型。玻尔说，电子绕核的角动量只能有一定的数值。这些值由公式给出

L = n h 2 π {/displaystyle L=n{/frac {h}{2pi }}}} $L=n{\frac {h}{2\pi }}$

哪儿

L=与水平面相关的角动量。

n=正整数。

h=普朗克常数。

原子的玻尔模型可以用来计算每一级电子的能量。电子通常会填满原子的最低数字状态。如果原子收到能量，例如，电流，电子将被激发到一个较高的状态。然后，电子会跌回较低的状态，并通过释放光子而失去其额外的能量。因为能级有特定的数值，所以光子会有特定的能级。用这种方式发出的光可以用棱镜分割成不同的颜色。每个元素都有自己的图案。霓虹灯的图案如旁边所示。

海森堡不确定性原理

1927年，维尔纳-海森堡发表了不确定性原理。该原理指出，不可能在不干扰被测物的情况下进行测量。它还对进行测量所造成的最小干扰进行了限制。

在宏观世界中，这些干扰的差别很小。例如，如果测量一个烧瓶中液体的温度，温度计在加热时会吸收少量的能量。这将导致最终读数的小误差，但这个误差很小，并不重要。

在量子力学中，事情是不同的。有些测量是通过观察散射光子的模式进行的。其中一个例子是康普顿散射。如果一个粒子的位置和动量都被测量，不确定性原理指出，在测量动量的精度和测量位置的精度之间有一个权衡。描述这种权衡的公式是：。

Δ x Δ p ↪Sm_2273↩ h {\displaystyle \Delta x,\Delta p \gtrsim h \qquad \qquad \qquad }。 $\Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad$

哪儿

Δp=动量的不确定性；

Δx=位置的不确定性；

h=普朗克常数。

发光二极管的颜色

在右图所示的电路中，发光二极管（LED）的压降取决于LED的材料。对于硅二极管来说，压降为0.6 V。然而对于LED来说，压降在1.8 V和2.7 V之间。这些信息使用户能够计算出普朗克常数。

在LED材料中，一个电子跳过势垒所需的能量由以下公式给出。

E = Q e V L {displaystyle E=Q_{e}V_{L}}}，}。 $E=Q_{e}V_{L}\,$

哪儿

_Qe是一个电子上的电荷。

_VL是LED上的电压降。

当电子再次衰变回来时，就会发出一个光子。光子的能量由光电效应中使用的同一方程式给出。如果将这些方程结合起来，光的波长和电压的关系为

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}}}},}。 $\lambda ={\frac {hc}{V_{L}Q_{e}}}\,$

根据这个关系可以计算出下表。

颜色	波长 (nm)	电压
红灯	650	1.89
绿灯	550	2.25
蓝光	470	2.62

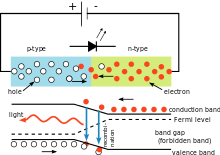
简单的LED电路，说明普朗克常数的使用。发出的光的颜色取决于二极管上的电压降。光的波长可以用普朗克常数来计算。

氖的可见光谱。每条线代表一对不同的能级。

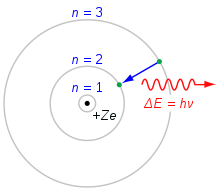
玻尔的原子模型。一个电子从n=3壳下降到n=2壳失去能量。这种能量是作为一个单一的光子带走。

普朗克常数的值和公斤的重新定义

自从它被发现以来，h的测量结果已经变得更好了。普朗克首先报出h的值是6.55×10^-27埃格-秒。这个值在当前值的5%以内。

截至2014年3月3日，h的最佳测量值在si单位是6.62606957×10^-34 J-s。cgs单位的等效数字是6.62606957×10^-27 erg-sec。h的相对不确定度为4.4×10-⁸。

减少的普朗克常数（ħ）是一个值，有时在量子力学中使用。它的定义是

↪Ll_210F↩ = h 2 π {\displaystyle \hbar ={frac {h}{2pi }}}} $\hbar ={\frac {h}{2\pi }}$ .

量子力学中有时用普朗克单位代替SI单位。在这个体系中，还原的普朗克常数的值为1，所以普朗克常数的值为2π。

普朗克常数现在可以用非常高的精度来测量。这使得国际生物圈计划考虑为公斤下一个新的定义。国际原型千克不再用于定义千克。取而代之的是，BIPM将普朗克常数定义为一个精确值。科学家们使用这个值以及米和秒的定义来定义公斤。

理论普朗克常数值

普朗克常数也可以通过数学方法得出。

h = μ 0 π 12 c 3 [q 0 [0.9163 a 0 ] 2 ] 。2 f 1 r 5 ⋅ s = 6.63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{[{q_{0}}{[0.9163a_{0}]}^{2}]^{2}}}{f_{1r}}^{5}cdot {s}=6.63\times 10^{-34}J\cdot s}。 $h={\frac {\mu _{0}\pi }{12c^{3}}}{[{q_{0}}{[0.9163a_{0}]}^{2}]^{2}}{f_{1r}}^{5}\cdot {s}=6.63\times 10^{-34}J\cdot s$

这里，μ 0 {displaystyle \mu _{0} $\mu _{0}$ }是自由空间的渗透率，c {displaystyle c} $c$ 是光速，q 0 {displaystyle q_{0} $q_{0}$ }是电子的电荷，a 0 {displaystyle a_{0} $a_{0}$ }是玻尔半径，f 1 r {displaystyle f_{1r} $f_{1r}$ }是氢原子中电子的旋转频率（f 1 r = 3.29×10 15 r e v / s ) {\displaystyle (f_{1r}=3.29\times 10^{15}rev/s)} $(f_{1r}=3.29\times 10^{15}rev/s)$ 。当这些常数值代入理论普朗克常数时，理论普朗克常数值正好等于实验值。

问题和答案

问：什么是普朗克常数？
答：普朗克常数是一个基本物理常数，它表示当一个光子的电磁波频率增加1时，其能量增加多少。

问：它是以谁命名的？
答：普朗克常数是以物理学家马克斯-普朗克命名的。

问：该常数的物理作用尺寸是多少？
答：普朗克常数的物理作用尺寸是能量乘以时间，或动量乘以距离。

问：它是如何用SI单位表示的？
答：在国际单位中，普朗克常数以焦耳秒(J⋅s)或(N⋅m⋅s)或(kg⋅m2⋅s-1)表示。

问：用这个量可以计算出哪些测量结果？
答：科学家们用这个量来计算普朗克长度和普朗克时间等测量值。

问：什么方程式描述了磁控管W和电子L？
答：磁控管W=Wb/2P 电子L=4C/3X=25e/3=（13U1d）。