调和级数

在数学中，谐波数列是分歧的无限数列。

∑n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {displaystyle sum _{n=1}^{infty }{frac {1}{n}}=1+{frac {1}{2}}+{frac {1}{3}}+{frac {1}{4}}}+{frac {1}{5}}+cdots }。 {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }

分歧的意思是，当你添加更多的项时，总和永远不会停止变大。它不会走向一个单一的有限值。

无限的意思是，你可以随时添加另一个术语。该系列没有最后一项。

它的名字来源于音乐中的谐波概念：振动弦的泛音的波长是弦的基本波长的1/2、1/3、1/4等。除第一项外，系列的每一项都是它两边项的谐波平均值。谐波平均数这个词组也来自音乐。

历程

和声数列分叉的事实最早是在14世纪由Nicole Oresme证明的，但后来被遗忘了。17世纪由Pietro Mengoli、Johann Bernoulli和Jacob Bernoulli给出了证明。

谐音序列一直被建筑师们所使用。在巴洛克时期，建筑师在平面图的比例、立面以及教堂和宫殿的建筑细节之间的关系中使用了它们。

分歧

关于谐波系列的发散性，有几个著名的证明。下面给出其中的几个。

比较试验

证明发散性的一种方法是将谐波数列与另一个发散性数列进行比较，其中每个分母都用2的次大幂代替。

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&。{}1+{/frac {1}{2}}+{/frac {1}{3}}}+{/frac {1}{4}}}+{/frac {1}{5}}+{/frac {1}{6}}}+{/frac {1}{7}}}+{/frac {1}{8}}}+{/frac {1}{9}}}+cdots {[12pt]geq {}&。1+{frac {1}{2}}+{frac {1}{color {red}{mathbf {4}。}}}+{{frac {1}{4}}+{frac {1}{color {red}{mathbf {8}。}}}+{frac {1}{color {red}{mathbf {8}。}}}+{frac {1}{color {red}{mathbf {8}。}}}+{{frac {1}{8}}+{frac {1}{color {red}{mathbf {16}。}}}+cdots ndend{aligned}}}。 {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}}

谐波系列的每一个项都大于或等于第二个系列的相应项，因此，谐波系列的和一定大于或等于第二个系列的和。然而，第二个系列的和是无限的。

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ =∞ {begin{aligned}&{}1+/left({frac {1}{2}}/right)+/left({frac {1}{4}}/!+！{frac {1}{4}}right)+\left({frac {1}{8}}}!{frac {1}{16}}right)+cdots ={}&1+{frac {1}{2}}+{frac {1}{2}}+{frac {1}{2}}+{frac {1}{2}}+{frac {1}{2}}+{frac {1}{2}}}+cdots =infty end{aligned}}}}}。 {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}

由此可见（通过比较检验），谐波系列的和也一定是无限的。更准确地说，上述比较证明

∑n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle ∑sum _{n=1}^{2^{k}}{\frac {1}{n}}}\geq 1+{\frac {k}{2}}}。 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}

对于每一个正整数k。

这个证明由Nicole Oresme在1350年左右提出，被认为是中世纪数学的一个高峰。今天，它仍然是数学课上教授的标准证明。

整体测试

通过将谐波数列的和与一个不恰当的积分进行比较，可以证明谐波数列发生了偏离。考虑右图所示的矩形的排列。每个矩形的宽是1个单位，高是1/n个单位，所以无限个矩形的总面积就是谐波数列的和。

矩形的面积=1+1 2+1 3+1 4+1 5+⋯ {\displaystyle {\begin{array}{c}{{text{area of}}\{text{rectangles}}end{array}}=1+{\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{4}}}+{\frac {1}{5}}}+cdots }。 {\displaystyle {\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }

从1到无穷大的曲线y=1/x下的总面积由一个发散的不恰当积分给出。

曲线下的面积 = ∫ 1 ∞ 1 x d x = ∞ 。{displaystyle {begin{array}{c}{{text{area under}}{c}{text{area under}}{curve}}{array}}=int _{1}^{/infty }{frac {1}{x}}{frac {1}{x}}},dx=\infty .} {\displaystyle {\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .}

既然这个面积完全包含在矩形内，那么矩形的总面积也一定是无限的。这就证明了

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) 。{displaystyle /sum _{n=1}^{k}{/frac {1}{n}}}>/int _{1}^{k+1}{/frac {1}{x}}}/dx=ln（k+1）。} {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).}

这个论点的概括称为积分检验。

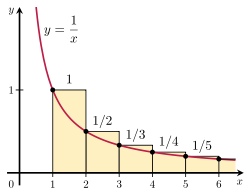
积分测试的说明。Zoom
积分测试的说明。

偏离率

谐波系列的分化非常缓慢。例如，前1043项之和小于100。这是因为系列的部分和具有对数增长。尤其是：

∑n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}leq (\ln k)+1}。 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}

其中γ是Euler-Mascheroni常数，εk ~ 1/2k，随着k的无穷大而接近0。莱昂哈德-欧拉既证明了这一点，又证明了只包括质数的互数的和也是发散的，即。

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ 。{displaystyle {sum _{p{text{ prime }}}{frac {1}{p}}={frac {1}{2}}}+{frac {1}{3}}}+{frac {1}{5}}}+{frac {1}{7}}}+{frac {1}{11}}}+{frac {1}{13}}}+{frac {1}{17}}}+cdots =infty .} {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .}

部分金额

前三十个谐音数

n

谐波系列的部分和，Hn。

 

分数

小数

相对规模

 

1

1

~1

1

 

 

2

3

/2

~1.5

1.5

 

 

3

11

/6

~1.83333

1.83333

 

 

4

25

/12

~2.08333

2.08333

 

 

5

137

/60

~2.28333

2.28333

 

 

6

49

/20

~2.45

2.45

 

 

7

363

/140

~2.59286

2.59286

 

 

8

761

/280

~2.71786

2.71786

 

 

9

7129

/2520

~2.82897

2.82897

 

 

10

7381

/2520

~2.92897

2.92897

 

 

11

83711

/27720

~3.01988

3.01988

 

 

12

86021

/27720

~3.10321

3.10321

 

 

13

1145993

/360360

~3.18013

3.18013

 

 

14

1171733

/360360

~3.25156

3.25156

 

 

15

1195757

/360360

~3.31823

3.31823

 

 

16

2436559

/720720

~3.38073

3.38073

 

 

17

42142223

/12252240

~3.43955

3.43955

 

 

18

14274301

/4084080

~3.49511

3.49511

 

 

19

275295799

/77597520

~3.54774

3.54774

 

 

20

55835135

/15519504

~3.59774

3.59774

 

 

21

18858053

/5173168

~3.64536

3.64536

 

 

22

19093197

/5173168

~3.69081

3.69081

 

 

23

444316699

/118982864

~3.73429

3.73429

 

 

24

1347822955

/356948592

~3.77596

3.77596

 

 

25

34052522467

/8923714800

~3.81596

3.81596

 

 

26

34395742267

/8923714800

~3.85442

3.85442

 

 

27

312536252003

/80313433200

~3.89146

3.89146

 

 

28

315404588903

/80313433200

~3.92717

3.92717

 

 

29

9227046511387

/2329089562800

~3.96165

3.96165

 

 

30

9304682830147

/2329089562800

~3.99499

3.99499

 

 

分歧谐系列的有限部分和。

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{frac {1}{k}},}。 {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},}

称为谐数。

Hn和ln n之间的差值趋近于欧拉-马舍罗尼常数。任何两个谐波数之间的差值都不是整数。除了H1=1，没有一个谐波数是整数。

相关系列

交替谐波系列

该系列

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {{displaystyle {sum _{n=1}^{infty}{frac {(-1)^{n+1}}{n}}=1-{frac {1}{2}}}+{frac {1}{3}}}-{frac {1}{4}}}+{frac {1}{5}}}-\cdots }。 {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots }

被称为交替谐波系列。这个数列通过交替数列检验收敛。特别是，其和等于2的自然对数。

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯=ln 2。{displaystyle 1-{/frac {1}{2}}+{/frac {1}{3}}-{/frac {1}{4}}+{/frac {1}{5}}-cdots =/ln 2.}。 {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.}

交替谐波数列虽然是有条件收敛的，但并不是绝对收敛的：如果数列中的项被系统地重新排列，一般来说，总和会变得不同，而且取决于重新排列的情况，甚至可能是无限的。

交替谐波数列公式是墨卡托数列的特例，是自然对数的泰勒数列。

由泰勒数列可以得出相关的数列，求出正切值。

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 。{displaystyle {sum _{n=0}^{/infty }{/frac {(-1)^{n}}{2n+1}}=1-{/frac {1}{3}}+{/frac {1}{5}}}-{/frac {1}{7}}}+cdots ={/frac {/pi }{4}}}.} {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.}

这就是所谓的莱布尼茨系列。

一般谐波系列

一般谐波系列的形式是

∑n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{frac {1}{an+b}},}。 {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},}

其中a≠0，b为实数，且b/a不是零或负整数。

通过与谐波系列的极限比较试验，所有的一般谐波系列也都出现了分歧。

P系列

谐波系列的一般化是p系列（或超谐波系列），定义为

∑n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p }}}} {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}}

当p=1时，p序列是谐波序列，它发生了发散。无论是积分检验还是Cauchy凝聚检验，都表明p系列对所有p>1时收敛（在这种情况下，它被称为过谐数列），对所有p≤1时发散。如果p>1，则p系列的和为ζ(p)，即在p处评价的黎曼zeta函数。

寻找p=2的和的问题被称为巴塞尔问题；Leonhard Euler证明了它是π2/6。p=3的和值被称为阿佩里常数，因为罗杰-阿佩里证明它是一个无理数。

ln系列

与p系列相关的是ln系列，定义为

∑n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}。 {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}

对于任何正实数p，这可以通过积分检验来证明，对于p≤1的情况下是发散的，但对于所有p>1的情况下是收敛的。

φ系列

对于任何一个凸的实值函数φ，使之

lim↪Zs_2006↩sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {displaystyle \limsup _{u/to 0^{+}}{frac {\varphi \left({frac {u}{2}}\right)}{varphi (u)}}<{frac {1}{2}}},}。 {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},}

该系列

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle _{n=1}^{\infty }varphi \left({\frac {1}{n}}\right)}。 {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)}

是收敛的。[]

随机谐波系列

随机谐波系列

∑n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{frac {s_{n}}{n}},}。 {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},}

其中Sn是独立的、相同分布的随机变量，其取值为+1和-1的概率为1/2，是概率论中一个著名的随机变量系列的例子，它以概率1收敛。这种收敛性的事实是由Kolmogorov三序列定理或与之密切相关的Kolmogorov最大不等式所带来的一个简单结果。阿尔伯塔大学的Byron Schmuland进一步研究了随机谐波数列的特性，并表明收敛数列是一个具有一些有趣特性的随机变量。特别是这个随机变量的概率密度函数在+2或在-2处评价时，其值为0.12499999999999999999999999764......，与1/8相差不到10-42。Schmuland的论文解释了为什么这个概率如此接近，但不完全是1/8。这个概率的精确值由无限余弦积积分C2除以π给出。

贫乏的谐波系列

去掉分母中任何地方出现的数字9的所有项的耗尽谐波数列可以被证明是收敛的，其值小于80。事实上，当所有包含任何特定数字串的项（在任何基数上）都被删除时，该数列就会收敛。

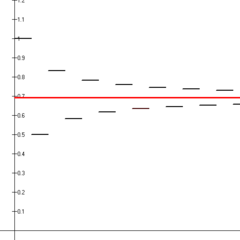
所示交替谐波系列的前十四个部分和（黑线段）收敛到2的自然对数（红线）。Zoom
所示交替谐波系列的前十四个部分和（黑线段）收敛到2的自然对数（红线）。

应用

谐波数列可能是反直觉的。这是因为它是一个发散的数列，尽管数列的项越来越小，并向零发展。谐波数列的发散性是一些悖论的来源。

  • "橡皮筋上的虫子"。假设一只虫子沿着一条无限弹性的一米长的橡皮筋爬行，同时橡皮筋被均匀拉伸。如果虫子每分钟行进1厘米，橡皮筋每分钟拉伸1米，那么虫子是否能到达橡皮筋的末端呢？答案一反常态，是"能"，因为n分钟后，虫子走过的距离与橡皮筋总长度的比值是

1 100 ∑k = 1 n 1 k 。{displaystyle {frac {1}{100}}/sum _{k=1}^{n}{frac {1}{k}}.} {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.}

因为随着n的变大，这个系列会任意变大，最终这个比率一定会超过1，这意味着蠕虫到达了橡皮筋的末端。然而，发生这种情况的n值必须非常大：大约e100，这个数字超过1043分钟（1037年）。虽然谐波系列确实发生了偏离，但其速度非常缓慢。

  • 吉普问题问的是：一辆载油量有限的汽车要穿越沙漠，沿途留下油滴，共需要多少燃料。汽车在给定的燃料量下能走的距离与谐波系列的部分和有关，谐波系列按对数增长。所以所需的燃料随着所需距离的增加而成倍增加。
  • 积木堆叠问题：给定一组相同的多米诺骨牌，可以将它们堆叠在桌子的边缘，使它们悬在桌子的边缘而不掉下来。反直觉的结果是，它们的堆叠方式可以使悬空的面积随你的要求而变大。也就是说，只要有足够的骨牌。
  • 一个游泳者，每次接触池壁的速度都会更快。游泳者以2米/秒的速度开始穿越10米长的泳池，每穿越一次，速度就会再增加2米/秒。理论上，游泳者的速度是无限的，但要达到这个速度所需要的过池次数就会变得非常大，例如，要达到光速（忽略狭义相对论），游泳者需要过池1.5亿次。与这个大数相反，达到某一速度所需的时间取决于任何给定的过池次数时的系列之和。

10 2 ∑k = 1 n 1 k 。{displaystyle {frac {10}{2}}/sum _{k=1}^{n}{frac {1}{k}}.} {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.}

计算得出，达到光速所需的时间只有97秒。

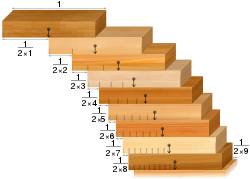
砌块堆叠问题：按照谐波系列排列的砌块，桥接任意宽度的裂缝。Zoom
砌块堆叠问题：按照谐波系列排列的砌块，桥接任意宽度的裂缝。

相关网页

  • 谐音递进
  • 互惠金额清单

问题和答案

问：什么是调和数列？
答：调和数列是一个无限发散的数列，其中每项都等于1除以它在数列中的位置。

问：一个数列是发散的，这意味着什么？
答：发散的意思是，当你增加更多的项时，总和永远不会停止变大，不会走向一个单一的有限值。

问：一个数列是无限的意味着什么？
答：无限意味着你总是可以增加另一个项，而且这个数列没有最后一项。

问：这个数列的名字是怎么来的？
答：这个数列的名字来自于音乐中的谐音概念，泛音的波长是弦的基本波长的1/2、1/3、1/4等。

问：什么是谐波平均值？
答：谐波平均值是指一个序列中的每一个项都等于其相邻项的谐波平均值。这句话也来自于音乐。

问：我们如何计算这个序列中的每个项？
答：这个序列中的每个项都可以通过用1除以它在序列中的位置（1/n）来计算。

AlegsaOnline.com - 2020 / 2023 - License CC3