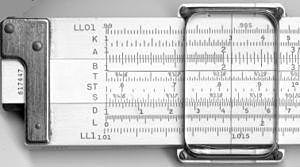
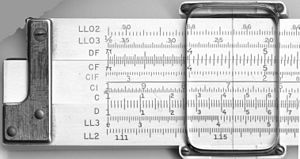
计算尺

基本概念

在最基本的形式上，滑尺使用两个对数刻度，可以快速地进行数字的乘法和除法。这些常见的运算在纸上进行时，会很耗时，而且容易出错。更复杂的滑动规则可以进行其他计算，如平方根、指数、对数和三角函数。

数学计算是通过将滑动中心条上的一个标记与固定条上的一个标记对齐来完成的。然后可以观察到其他标记的相对位置。与标记对齐的数字给出了积、商或其他计算结果的近似值。

用户根据头脑中的估计来确定结果中小数点的位置。在比较正式的计算中，用科学记号来跟踪小数点。计算中的加减步骤一般是在心里或纸上完成，而不是在滑尺上完成。

大多数滑动规则都有三个相同长度的线性条带。这些条带是平行排列的，并且相互交错，因此中心条带可以相对于其他两个条带进行长度上的移动。外侧的两个条带是固定的，因此它们的相对位置不会改变。

有些滑动规则（"双工"模型）的刻度在规则和滑条的两侧，有些在外条的一侧和滑条的两侧，还有些只在一侧（"单工"规则）。带有垂直对齐线的滑动光标用于在不相邻的刻度上找到相应的点，或者在双工模型中，在规则的另一侧。光标还可以在任何一个标尺上记录中间结果。

滑动规则上的光标

使用滑动规则进行计算

乘法

对数根据以下规则将乘除运算转化为加减运算 log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=log(x)+\log(y)} 和 log ( x / y ) = log ( x ) - log ( y ) {\displaystyle \log(x/y)=\log(x)-\log(y)} 。将上标尺向右移动距离为log ( x ) {\displaystyle \log(x)} 。通过匹配顶部刻度的开始与底部的标签x {\displaystyle x}，对准每个数字y {\displaystyle y}。，在位置log ( y ) {\displaystyle \log(y)}上标尺，在位置log ( x ) + log ( y ) {\displaystyle \log(x)+log(y)}下标尺。因为log ( x ) + log ( y ) = log ( x y ) {\displaystyle \log(x)+log(y)=log(xy)}。，这个位置在底部刻度上给出了x y {\displaystyle xy}。, x {\displaystyle x}和y {\displaystyle y}的乘积。例如，要计算3*2，上标尺上的1被移动到下标尺上的2。答案，6，从底层刻度上读出，其中3在顶层刻度上。一般来说，顶部的 1 会被移到底部的因子上，而答案会从底部读出，其中另一个因子在顶部。

操作可能会出现"偏离刻度"的情况；例如，上图显示，滑动规则没有将上刻度上的7定位在下刻度上的任何数字之上，因此它没有给出2×7的任何答案。在这种情况下，用户可以将上标尺向左滑动，直到它的右索引与2对齐，有效地乘以0.2而不是2，如下图所示。

在这里，滑动规则的使用者一定要记得适当调整小数点，以修正最后的答案。我们想找2×7，但却计算出0.2×7=1.4。所以真正的答案不是1.4而是14。重置滑片并不是处理2×7等会导致结果偏离尺度的乘法的唯一方法，还有一些其他方法。

• (1)使用双十刻度A、B。
• (2)使用折叠式刻度。在本例中，将C的左1与D的2相对，在CF上将光标移至7，从DF中读取结果。
• (3)使用CI倒标尺。将CI刻度上的7置于D刻度上的2之上，然后从D刻度上读出结果，在CI刻度上的1之下。由于1出现在CI量表的两处，所以其中一处总是在刻度上。
• (4)同时使用CI倒标和C标。将CI的2与D的1排成一行，从D中读出结果，在C刻度的7下面。

方法1容易理解，但会损失精度。方法3的优点是只涉及两个刻度。

部门

下面的插图演示了5.5/2的计算方法。上标尺上的1位于商的上方，即2.75。做除法的方法不止一种，但这里介绍的方法有一个优点，就是最后的结果不能偏离刻度，因为人们可以选择使用两端的1。

其他业务

除了对数标度外，一些滑动规则还有其他数学函数编码在其他辅助标度上。最受欢迎的是三角函数，通常是正弦和正切、普通对数（log10）（用于在倍数刻度上取值的对数）、自然对数（ln）和指数（^ex）刻度。一些规则包括毕达哥拉斯比例尺，用于计算三角形的边，以及用于计算圆的比例尺。其他规则的特点是计算双曲函数的比例尺。在线性规则中，标度及其标记是高度标准化的，通常只在包括哪些标度和顺序方面出现差异。

A, B	二阶对数
C, D	单十年对数标度
K	三段论标尺
CF、DF	C和D刻度的"折叠"版本，从π开始而不是从统一开始；这在两种情况下很方便。首先，当用户猜测一个乘积会接近10，但不确定它是略小于还是略大于10时，折叠式刻度就避免了偏离刻度的可能性。其次，通过将起点π而不是10的平方根，乘以或除以π（如科学和工程公式中常见的）被简化。
CI、DI、DIF	"倒立标尺
S	用于求D刻度上的正弦和余弦值
T	的切线和余切线。
ST、SRT	弧度换算
L	线性标度，与C和D标度一起用于求10次方对数和10次方幂。
LLn	对数集对数标度
Ln	线性标度，与C和D标度一起用于寻找自然（基数e）对数和e x {\displaystyle e^{x}}。

 

K&E 4081-3滑尺正面和背面的刻度。

Gilson在1931年制造的二进制滑动法则执行的加减法功能仅限于分数。

根与权

有单十年（C和D）、双十年（A和B）和三十年（K）的尺度。计算x 2 {displaystyle x^{2}}。例如，在D标尺上定位x，在A标尺上读出它的平方。反转这个过程可以找到平方根，同样也可以找到3、1/3、2/3和3/2的幂。当基数x在其刻度上不止一处时，必须注意。例如，A标尺上有两个九，要找9的平方根，就用第一个，第二个就可以得到90的平方根。

对于x y {displaystyle x^{y}}问题，使用LL标度。当存在多个LL刻度时，使用带有x的那个刻度。首先，将C标尺上最左边的1与LL标尺上的x对齐。然后，在C标尺上找到y，并向下找到带有x的LL标尺。该刻度将指示答案。如果 y 是"不在刻度上"，则找到 x y / 2 {\displaystyle x^{y/2}}，并使用上述的 A 和 B 刻度将其平方。

三角学

S、T和ST刻度用于三角函数和三角函数的倍数，用于以度为单位的角度。许多幻灯规则的S、T、ST刻度都标有度和分。所谓的decitrig模型是用度的小数分数来代替。

对数和指数

基数10的对数和指数是用L刻度来找的，这是线性的。有的滑道规则有Ln刻度，是针对基数e的。

Ln标尺是由11年级的学生Stephen B. Cohen在1958年发明的。最初的目的是让用户在Ln量表上选择一个指数x（范围为0到2.3），然后在C（或D）量表上读出^ex，在CI（或DI）量表上读出^e-x。皮克特公司获得了该量表的专有权。后来，发明人在Ln刻度上创造了一组"标记"，以将范围扩大到2.3的限制之外，但Pickett从未将这些标记纳入其任何滑动规则。^[]

加法和减法

幻灯片规则一般不用于加减法，但还是可以用两种不同的技巧来做加减法。

在C和D（或任何可比的尺度）上进行加减法的第一种方法需要将问题转化为除法的问题。对于加法，两个变量的商加上1乘以除数等于它们的和。

x + y = ( x y + 1 ) y {displaystyle x+y=/left({/frac {x}{y}}+1/right)y}。

对于减法来说，两个变量的商减一乘以除数等于它们的差。

x - y = ( x y - 1 ) y {displaystyle x-y=/left({/frac {x}{y}}-1/right)y}。

这种方法类似于高速电子电路中的对数系统的加减法技术，在专门的计算机应用中，如重力管（GRAPE）超级计算机和隐藏马尔科夫模型。

第二种方法使用某些型号上可用的滑动线性L刻度。通过向左滑动光标（用于减法）或向右滑动光标（用于加法）进行加法和减法，然后将滑块返回到0，读取结果。

物理设计

标准线性规则

滑尺的长度是以刻度的标称长度来引用的。最常见的"10英寸"型号上的刻度实际上是25厘米长，因为它们是按照公制标准制作的，尽管有些规则提供了稍微延长的刻度，以简化结果溢出时的操作。袖珍规则通常为5英寸。几米长的模型被出售，挂在教室里用于教学。[1]

一般情况下，分部标记一个刻度的精度为两个重要数字，用户估算第三个数字。一些高端滑尺具有放大光标，使标记更容易看清。这种光标可以有效地将读数的精度提高一倍，使10英寸的滑尺与20英寸的滑尺一样好用。

还开发了其他各种便利条件。三角尺有时采用双标，黑红两色，角度互补，即所谓"达姆施塔特"式。双面滑尺的规则往往与背面的一些刻度重复。为了获得更高的精度，刻度常常被"拆分"。

为各种形式的工程、商业和银行发明了专门的滑动规则。这些规则通常将常见的计算直接表示为特殊的刻度，例如贷款计算、最佳采购量或特殊的工程方程。例如，Fisher Controls公司分发了一个定制的滑动规则，用于解决选择工业流量控制阀适当尺寸的方程。^[]

圆滑规则

圆滑规则有两种基本类型，一种是有两个游标（左），另一种是有一个活动圆盘和一个游标（右）。双游标版本通过在游标围绕转盘旋转时保持游标之间的固定角度来进行乘除运算。单游标版本的操作方式更像标准的滑尺，通过刻度的适当排列。

圆形滑尺的基本优点是工具的最长尺寸减少了约3倍（即π）。例如，10厘米圆形的外刻度的最大精度将等于30厘米的普通滑尺。圆形滑尺还可以消除"偏离尺度"的计算，因为尺度被设计成"环绕"的；当结果接近1.0时，它们永远不必重新定向--规则总是在尺度上。然而，对于非周期性的非螺旋形刻度，如S、T和LL的刻度，刻度长度要缩短，以便为端部边缘留出空间。

圆形滑块规则在机械上更坚固，移动更平稳，但其刻度对准精度对中心枢轴的对中很敏感；枢轴偏离中心0.1毫米的微小误差会导致0.2毫米的最差对准误差。然而，枢轴可以防止表面和光标的划伤。最高精度的刻度被放置在外环上。高端圆规没有采用"分体式"刻度，而是采用螺旋式刻度来进行更复杂的操作，比如对数的刻度。一款8英寸的高端圆规有一个50英寸的螺旋对数刻度。

圆形滑块规则的主要缺点是难以沿旋转圆盘定位数字，而且刻度数量有限。圆滑规则的另一个缺点是不太重要的刻度离中心较近，精度较低。大部分学生在直线滑尺上学会了滑尺的使用，并没有找到转换的理由。

世界各地仍在日常使用的一种滑尺是E6B。这是一种圆形滑尺，最早是在20世纪30年代为飞机飞行员创造的，用于帮助进行死角计算。借助印在框架上的刻度，它还可以帮助完成时间、距离、速度和温度值的换算、罗盘误差和计算燃料使用量等杂项工作。所谓的"祈祷轮"在飞行商店中仍然可以买到，并且仍然被广泛使用。虽然GPS减少了空中导航的死角计算，手持计算器也取代了它的许多功能，但E6B仍然被广泛地用作主要或备用设备，大多数飞行学校都要求学生在一定程度上掌握它。

1952年，瑞士钟表公司百年灵推出了一款集成圆形滑尺的飞行员腕表，专门用于飞行计算：百年灵Navitimer。这款被百年灵称为"导航电脑"的Navitimer圆形规则具有空速、爬升/下降速率/时间、飞行时间、距离和燃料消耗功能，以及公里-海里和加仑-升燃料量转换功能。

材料

传统的滑轨规则是由硬木（如桃花心木或黄杨木）和玻璃、金属等材料制成的。至少有一种高精度的仪器是由钢制成的。

1895年，日本的一家公司Hemmi开始用竹子制作滑尺，这种竹子具有尺寸稳定、强度大、天然自润滑等优点。这种竹制滑尺于1933年9月在瑞典问世[2]，德国可能只早一点。当时的刻度是用赛璐珞或塑料制成的。后来的滑尺是用塑料制成，或用塑料涂铝。后来的光标是亚克力或聚碳酸酯，在特氟隆轴承上滑动。

所有高级滑轨规则都刻有数字和刻度，然后用油漆或其他树脂填充。彩绘或印制的滑尺被视为劣质品，因为标记可能会磨损。尽管如此，Pickett，可能是美国最成功的滑竿公司，制造了所有的印刷刻度。高级滑尺包括巧妙的卡扣，这样滑尺就不会因意外而散架，还有保险杠，以保护刻度和游标不在石板上摩擦。对于雕刻的标记，推荐的清洁方法是用钢棉轻轻擦洗。对于油漆过的滑轨规则，以及胆小的人，可以使用稀释的商业擦窗液和软布。

百年灵Navitimer 腕表，带圆形滑轨。


一条简单的圆形滑尺，由日本东京简明株式会社制造，只有反比例、正比例和立方比例。背面是38个公制/英制换算系数的方便列表。


皮克特圆形滑尺有两个游标。直径4.25英寸/10.9厘米）反面有额外的刻度和一个游标。

历程

滑尺是在1620-1630年左右发明的，在约翰-纳皮尔发表对数概念后不久。牛津大学的埃德蒙-冈特（Edmund Gunter）开发了一种带有单一对数刻度的计算装置，配合其他测量工具，可用于乘法和除法。1624年，英国数学家埃德蒙-温盖特（Edmund Wingate，约1593-1656年）在巴黎出版了一本名为《L'usage de la reigle de proportion en l'arithmetique & geometrie》的书，首次对这种刻度进行了描述。书中有一个双标尺，一边是对数标尺，另一边是表格标尺。1630年，剑桥的威廉-奥特雷德发明了一种圆形的滑尺，1632年，他将两根冈特尺组合在一起，用手握住，制成了一种装置，这就是现代滑尺的辨识度。和他在剑桥的同时代人艾萨克-牛顿一样，奥赫特雷德也将自己的想法私下传授给学生，但迟迟没有发表，和牛顿一样，他也卷入了一场关于优先权的激烈争论，他曾经的学生理查德-德拉曼和温盖特的事先主张。奥特雷德的思想只是在1632年和1653年他的学生威廉-福斯特的出版物中才被公开。

1677年，亨利-科格肖尔创造了一种用于测量木材的两英尺长的折叠尺，称为科格肖尔滑尺。他对这一工具的设计和使用，使滑尺有了数学探究之外的用途。

1722年，华纳推出了二度和三度刻度，1755年，埃弗拉德加入了一个倒置刻度；包含所有这些刻度的滑尺通常被称为"多相"规则。

1815年，彼得-罗杰发明了对数滑动规则，其中包括一个显示对数的刻度。这使得用户可以直接进行涉及根和指数的计算。这对小数幂特别有用。

现代形式

更现代的形式是由法国炮兵中尉阿梅迪-曼海姆在1859年创造的，"他很幸运，他的规则由一家全国知名的公司制作，并被法国炮兵采用"。大约在那个时候，随着工程成为一种公认的专业活动，滑尺在欧洲得到了广泛的应用。直到1881年，当Edwin Thacher在那里推出圆柱形规则时，它们才在美国普及。1891年，William Cox发明了复式尺，由纽约的Keuffel和Esser公司生产。

天文工作也需要精细的计算，在19世纪的德国，一个天文台使用了一条长约2米的钢制滑尺。它连接着一个显微镜，使其精确度达到小数点后6位。

在第二次世界大战中，需要快速计算的轰炸机手和导航员经常使用专门的滑尺。美国海军的一个办公室实际上设计了一个通用的滑尺"底盘"，它有一个铝制机身和塑料游标，可以将赛璐珞卡片（双面印刷）放入其中，进行特殊计算。这个过程是为了计算飞机的航程、燃料使用量和高度而发明的，后来又被改编成许多其他用途。

在整个20世纪50年代和60年代，滑尺是工程师职业的象征（就像听诊器象征医学职业一样）。^[]德国火箭科学家维尔纳-冯-布劳恩在二战后移居美国从事美国太空计划时，带了两把20世纪30年代的老式雀巢滑尺。在他的一生中，他从未使用过任何其他袖珍计算设备，滑尺完全可以为他提供快速估算火箭设计参数和其他数字的服务。根据皮克特N600滑尺盒上的广告，铝制皮克特品牌的滑尺在阿波罗五次太空任务中被携带，包括登月[3]。

一些工程专业的学生和工程师将十英寸的滑尺装在腰包里，甚至到了1970年代中期，这种情况在校园里也很常见。学生们也可能在家里或办公室里保留一条十英寸或二十英寸的尺子，用于精密工作，同时随身携带一条五英寸的袖珍滑尺。

2004年，教育研究人员David B. Sher和Dean C. Nataro设想了一种基于prosthaphaeresis的新型滑动规则，这是一种比对数更早的快速计算产品的算法。然而，除了最初的原型之外，人们对构建一个的实际兴趣不大。[4]

跌幅

随着20世纪50年代电子计算机这种新的但非常稀缺的资源在60年代被技术工人广泛使用，滑步法则的重要性开始减弱。1957年Fortran的问世使计算机成为解决中等规模数学问题的实用工具。IBM公司推出了一系列更经济实惠的计算机，IBM 650（1954年）、IBM 1620（1959年）、IBM 1130（1965年），针对的是科学和工程市场。John Kemeny的BASIC编程语言（1964年）使学生们很容易使用计算机。1965年，DEC PDP-8小型计算机问世。

计算机也改变了计算的性质。有了幻灯片规则，人们非常强调用代数来把表达式变成最可计算的形式。幻灯片规则的用户只需简单地近似或删除小项，以简化计算。Fortran允许从教科书中输入复杂的公式，而不需要重新计算。数值积分往往比试图为困难的问题找到封闭式的解决方案要容易得多。年轻的工程师要求计算机时间来解决一个本可以通过在滑尺上刷几下就能解决的问题，这成了一个幽默的陈词滥调。许多计算机中心的墙上都挂着一个带框的滑尺，上面写着"紧急情况下，打碎玻璃"。

用电子学取代滑尺的另一个步骤是开发了科学和工程用的电子计算器。首先是1965年推出的Wang Laboratories LOCI-2，它使用对数乘除法，以及1968年推出的Hewlett-Packard HP-9100。HP-9100除了指数和对数外，还有三角函数（sin、cos、tan）。它采用CORDIC（坐标旋转数字计算机）算法，仅用移位和加法运算就可以计算三角函数。这种方法促进了越来越小的科学计算器的发展。

滑尺的最后一颗钉子是推出了袖珍型科学计算器，其中1972年的惠普HP-35是第一款。这种计算器被称为"滑尺"计算器，因为它们可以实现滑尺上的大部分或全部功能。即使是几百美元，对大多数学生来说也是昂贵的。虽然专业的滑尺也可能相当昂贵，但药店通常以20美元以下的价格出售基本的塑料模型。但到了1975年，基本的四功能电子计算器可以用50美元以下的价格购买。到1976年，TI-30提供的科学计算器价格低于25美元。在这之后，随着小型科学计算器变得经济实惠，滑尺的市场迅速枯竭。

TI-30


工程师使用滑尺。注意背景中的机械计算器。


威廉・奥夫特雷德（1575-1660），圆滑尺的发明者。

优势

• 滑尺往往能缓和"假精度"和意义的谬误。滑动规则的使用者可获得的典型精度约为精度的3位。这与大多数可用于输入工程公式的数据有很好的对应关系。当使用现代袖珍计算器时，精度可以显示到小数点后7位或更多，而实际上结果永远不可能比输入的数据更精确。
• 幻灯片规则需要不断估计结果的数量级。在滑动规则上，1.5×30（等于45）与1,500,000×0.03（等于45,000）的结果是一样的。工程师要不断地确定结果的合理性，当粗心地将数字输入计算机程序或计算器时，就会失去这种感觉。
• 当执行同一数字的乘法或除法顺序时，往往只需看一眼滑尺就能确定答案，而不需要进行任何操作。这在计算百分比时特别有用，例如，计算考试分数，或比较价格时，例如，以每公斤美元为单位。使用滑尺可以在不需要动手的情况下，一目了然地进行多个速度-时间-距离的计算。
• 滑尺不靠电。
• 滑尺是一种容易复制的技术。从一个给定的滑尺例子中，一个有能力的工匠可以用简陋的材料，用非工业化的工艺建造更多的滑尺。
• 幻灯片规则是高度标准化的，所以当切换到不同的规则时，不需要重新学习任何东西。
• 幻灯片规则是多功能的，可以在人类用户可能会降低灵活性的情况下（例如，由于需要戴防护手套）进行操作。相反，计算器在这种情况下很难操作--滑动规则不太可能导致类似于误按计算器上的错误按钮的错误。
• 滑动规则可以用硬纸板或纸做。许多用纸板制作的免费图表或专门的计算装置，实际上是专门的直线或圆滑规则。

将滑尺与电子计算器一起使用的一个好处是，一个重要的计算可以通过在两个工具上进行检查；因为两个工具是如此的不同，几乎没有机会犯同样的错误两次。

缺点

• 误差可能来自于机械的不精确性。
• 由于模拟输入和输出，使用滑尺进行计算的精度有限。相反，由于离散的数字输入和浮点电子运算，即使是小型的现代计算器，其输出分辨率也至少有六位数。

相关网页

• 算盘
• 对数