点积

在数学中，点积是一个将两个向量作为输入，并将一个标量数字作为输出的运算。返回的数字取决于两个向量的长度，以及它们之间的角度。这个名字来自于通常用来表示这个操作的中间点"-"；另一个名字标量积强调了结果的标量（而不是矢量）性质。

点积与交叉积形成对比（在三维空间），交叉积的结果是一个矢量。

定义

两个向量a = [a₁ , a₂ , ..., a_n ] 和b = [b₁ , b₂ , ..., b_n ] 的点积定义为。

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {displaystyle \mathbf {a} \cdot \mathbf {b} =sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}] $\mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

其中Σ表示求和符号（所有项的总和），n是矢量空间的维度。

在维度2中，向量[a,b]和[c,d]的点积是ac+bd。同样，在维度3中，向量[a,b,c]和[d,e,f]的点积是ad + be + cf。例如，两个三维向量[1, 3, -5]和[4, -2, -1]的点积是

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) )+ {displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3。 $[1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.$

几何学解释

在欧几里德几何学中，点积、长度和角度是相关的。对于一个向量a，点积a-a是a的长度的平方，或

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=left\|\mathbf {a} \right\|^{2} }}=left\|mathbf {a}\right\|^{2}}。 ${\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}$

其中||a||表示a的长度（幅度）。更一般地说，如果b是另一个矢量

a ⋅ b = ‖ a ‖ b ‖ cos θ {displaystyle \mathbf {a} cdot \mathbf {b} =\left\||mathbf {a} `right\|,`left\|mathbf {b} `left\|mathbf {b} `left\Right\|cos theta\,} $\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,$

其中||a||和||b||表示a和b的长度，θ是它们之间的角度。

这个公式可以重新排列，以确定两个非零向量之间的角度大小。

θ = arccos ( a ⋅ b ‖ a ‖ b ‖ ) {\displaystyle\theta =\arccos \left({frac {{mathbf {a}}\cdot {mathbf {b}}}{left\|{mathbf {a}}\right\|left\|{mathbf {b}}}\right\|}}\right) } $\theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)$

我们也可以首先通过除以它们的幅度将向量转换成单位向量。

a ^ = a ‖ a ‖ {\displaystyle {boldsymbol {hat {a}}={frac {mathbf {a}}{\left\|{mathbf {a}}\right\|}}}。 ${\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}$

则角度θ由以下公式给出

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle\theta =arccos({\boldsymbol {hat {a}}\cdot {\boldsymbol {hat {b}})}。 $\theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})$

由于90°的余弦为零，两个正交（垂直）矢量的点积总是为零。此外，当且仅当两个向量的点积为零，并且它们的长度都不为零时，才可以认为是正交的。这个属性提供了一个简单的方法来测试正交性的条件。

有时这些属性也被用来定义点积，特别是在2维和3维中；这个定义等同于上述定义。对于更高的维度，该公式可以用来定义角度的概念。

几何特性依赖于基础是正交的，即由具有单位长度的一对垂直向量组成。

标量投射

如果a和b的长度都是1（即，它们是单位向量），它们的点积只是给出了它们之间的角度的余弦。

如果只有b是单位向量，那么点积a-b就可以得到|a|cos(θ)，即a在b方向上的投影大小，如果方向相反，就用减号。这被称为a对b的标量投影，或a在b方向的标量分量（见图）。点积的这一特性有几个有用的应用（例如，见下一节）。

如果a和b都不是单位向量，那么a在b方向的投影的大小，例如，将是a - (b / |b|) ，因为b方向的单位向量是b / |b|。

旋转

用旋转矩阵R对向量a进行旋转，就可以得到a的旋转。这个矩阵乘法只是点乘序列的紧凑表示。

例如，让

B₁ = {x, y, z}和B₂ = {u, v, w}是同一空间R³ 的两个不同的正态基，B₂ 只是通过旋转B₁ 得到。
a₁ = (a_x , a_y , a_z ) 代表向量a在B₁ 。
a₂ = (a_u , a_v , a_w )代表同一向量的旋转基础B₂ 。
u₁ , v₁ , w₁ 是旋转的基向量u, v, w，用B₁ 表示。

然后，从B₁ 到B₂ 的旋转按如下方式进行。

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1⋅ a 1 v 1⋅ a 1 w 1⋅ a 1 ] = [ a u a v a w ] 。{\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf{v}_{1}cdot {a}_{1}\{mathbf {w}_{1}\cdot {a}_{1}\end{bmatrix}}={begin{bmatrix}a_{u}\a_{v}\a_{w}\end{bmatrix}}。} ${\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.$

请注意，旋转矩阵R是通过使用旋转基向量u₁ , v₁ , w₁ 作为其行来组装的，这些向量是单位向量。根据定义，Ra₁ 由R的三行中的每一行与向量a₁ 之间的点积序列组成。这些点积中的每一个都决定了a在旋转基向量方向上的标量分量（见上节）。

如果一个₁ 是行向量，而不是列向量，那么R必须在其列中包含旋转的基向量，并且必须对一个₁ 进行后乘。

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1⋅ a 1 v 1⋅ a 1 w 1⋅ a 1 ] = [ a u a v a w ] 。{displaystyle {mathbf {a}}_{2}={mathbf {a}}_{1}{mathbf {R}}={begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={begin{bmatrix}{mathbf {u}}_{1}\cdot {mathbf {a}}_{1}&{mathbf {v}}_{1}\cdot {mathbf {a}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.} ${\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.$

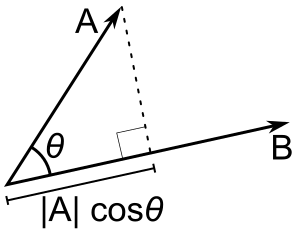
A - B = |A| |B| cos(θ)。 |A| cos(θ)是A对B的标量投影。

物理学

在物理学中，量值是物理意义上的标量，即独立于坐标系的物理量，表示为一个数值与一个物理单位的乘积，而不仅仅是一个数字。点积在这个意义上也是一个标量，由公式给出，独立于坐标系。例子。

机械功是力和位移矢量的点积。
磁通量是磁场和面积向量的点积。
体积流速是流体速度和面积向量的点积。

属性

如果a、b、c是实数向量，r是标量，则以下性质成立。

点积是交换性的。

a ⋅ b = b ⋅ a . {displaystyle\mathbf {a} cdot \mathbf {b} =mathbf {b} .\cdot /mathbf {a} 。} $\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .$

点积是对矢量加法的分配。

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c 。{displaystyle {mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} 。+mathbf {a} \cdot \mathbf {c} .} $\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

点积是双线性的。

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) 。{displaystyle {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ) 。} $\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

当与一个标量值相乘时，点积满足。

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b})} $(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )$

(这后两个属性是由前两个属性得出的)。

当且仅当a-b=0时，两个非零矢量a和b是垂直的。

与普通数字的乘法不同，如果ab=ac，那么b总是等于c，除非a为零，但点积不遵守取消法则。

如果a-b=a-c且a≠0，那么我们可以根据分配律写出：a-（b-c）=0；上面的结果说这只是意味着a垂直于（b-c），这仍然允许（b-c）≠0，因此b≠c。

只要基是正交的，点积在基的等距变化下是不变的：旋转、反射和组合，保持原点不变。上面提到的几何学解释依赖于这一属性。换句话说，对于一个具有任意维数的正交空间，点积在基于正交矩阵的坐标变换下是不变的。这对应于以下两个条件。

新的基础又是正态的（即在旧的基础上表达的是正态的）。
新的基数向量与旧的基数具有相同的长度（即以旧的基数为单位的长度）。

如果a和b是函数，那么a-b的导数是a'-b+a-b'

三重产品扩展

这是一个非常有用的特性（也被称为拉格朗日公式），涉及点积和交叉积。它被写成

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} ) =\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\ǞǞ(ǞǞǞǞǞ)} $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$

更容易记住的是 "BAC减去CAB"，记住哪些向量是点在一起的。这个公式通常用于简化物理学中的矢量计算。

几何解释的证明

考虑R的元素ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . .+ v n e ^ n .{displaystyle {v} =v_{1}\mathbf {hat {e}} _{1}+v_{2}\mathbf {hat {e}} ._{1}+v_{2}\mathbf {hat {e}} _{2}+...。_{2}+...+v_{n}\mathbf {hat {e}}._{n}.\,} $\mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,$

重复应用毕达哥拉斯定理，可以得到其长度|v|。

| v | 2 = v 1 2 + v 2 2 + . . .+ v n 2 。{displaystyle |mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v n 2 。|^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} $|\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,$

但这与

v ⋅ v = v 1 2 + v 2 2 + . . .+ v n 2 , {displaystyle\mathbf {v}\cdot\mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},}。 $\mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,$

所以我们得出结论，将一个向量v与它本身的点积得到该向量的平方长度。

定理1

v ⋅ v = | v | 2 。{displaystyle {mathbf {v} {cdot {mathbf {v} =|\mathbf {v}} 。|^{2}.\,} $\mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,$

现在考虑从原点延伸的两个矢量a和b，它们之间相隔一个角度θ。第三个矢量c可以定义为

c = d e f a - b 。{fnTahomafs10bord0shad01cH00FFFF}{displaystyle}mathbf {c}.\ {fnTahomafs10bord0shad01cH00FFFF}{stackrel {fnTahomafs10bord0shad01cH00FFFF}}}{stackrel {mathrm {def}}.}{=}}\mathbf {a} -mathbf {b} .\，}。 $\mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,$

形成一个边长为a、b、c的三角形。根据余弦定律，我们有

| c | 2 = | a | 2 + | b | 2 - 2 | a | b | cos θ。{fnTahomafs10bord0shad01cH00FFFF}{displaystyle}|mathbf {c}}}}}^{2}=|mathbf {a}.|^{2}=|mathbf {a}|^{2}+|mathbf {c}。|^{2}+|mathbf {b}|^{2}-2|mathbf {b}。|^{2}-2||mathbf {a}||mathbf {b}|||mathbf {b}||mathbf {b}|cos /theta.,} $|\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

根据定理1，用点积代替长度的平方，我们得到

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | b | cos θ 。\cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} 。\2||||||||||||||||||||||||||||||||||||||||||||||mathbf {b}||mathbf {b}。|\ $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$ (1)

但由于c≡a-b，我们也有

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c｝\cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )cdot (\mathbf {a} -\mathbf {b} )， } $\mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,$ 。

根据分配律，它扩展为

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) 。\cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} 。\cdot \mathbf {b} -2(\mathbf {a} cdot \mathbf {b} ).\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,$ (2)

合并两个c-c方程，（1）和（2），我们得到

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | b | cos θ。{displaystyle {mathbf {a} cdot {mathbf {a} +mathbf {b}}。\cdot \mathbf {b} -2(\mathbf {a} \mathbf {b} )=\mathbf {a} \mathbf {a} +\mathbf {b)\2||||||||||||||||||||||||||||||||||||||||||||||mathbf {b}||mathbf {b}。|cos /theta.,} $\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

从两边减去a-a+b-b，再除以-2，就可以得出结论。

a ⋅ b = | a | b = cos θ 。{displaystyle {mathbf {a} {cdot {mathbf {b} =|||mathbf {a} {displaystyle {mathbf {b} =|||mathbf {b}。|cos θ ...,}。 $\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Q.E.D.

归纳

内积将点积推广到抽象的向量空间，通常用⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} 表示。\矩形 } $\langle \mathbf {a} \,,\mathbf {b} \rangle$ .由于点积的几何解释，向量a在这样一个内积空间中的规范||a||定义为

‖ a ‖ = ⟨ a , a ⟩ {displaystyle\|\mathbf {a}\|={sqrt {langle\mathbf {a}\,, \mathbf {a} rangle }}. $\|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}$

这样，它概括了长度，而两个向量a和b之间的角度θ由

cos θ = ⟨ a , b ⟩ ‖ a ‖ b ‖ 。{displaystyle {cos {theta }={frac {langle {mathbf {a} },,{mathbf {b} }.\langle }{|\mathbf {a}\|,|\mathbf {b}\|\|}}.} $\cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.$

特别是，如果两个向量的内积为零，则被认为是正交的。

⟨ a , b ⟩ = 0. {displaystyle \langle \mathbf {a} \,,\mathbf {b} =0.\矩形=0.}。 $\langle \mathbf {a} \,,\mathbf {b} \rangle =0.$

对于有复数项的向量，使用给定的点积定义会导致相当不同的几何特性。例如，一个向量与它本身的点积可以是一个任意的复数，并且可以是零，而该向量不是零向量；这又会对长度和角度等概念产生严重后果。许多几何特性可以被挽救，但代价是放弃标量积的对称和双线性特性，方法是替代性地定义为

a ⋅ b = ∑ a i b i ¯ {\displaystyle\mathbf {a} \cdot\mathbf {b} =\sum {a_{i}{overline {b_{i}}}}} $\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}$

其中b_i 是b_i 的复共轭。那么任何矢量与自身的标量积都是一个非负实数，而且除了零矢量之外都是非零。然而这个标量积在b中不是线性的（而是共轭线性的），而且标量积也不是对称的，因为

a ⋅ b = b ⋅ a ¯ {displaystyle \mathbf {a} cdot \mathbf {b} ={overline {mathbf {b}}.\జజజజజ}} $\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}$ 。

然而，这种类型的标量积是相当有用的，并导致了赫米特形式和一般内积空间的概念。

Frobenius内积将点积推广到矩阵。它被定义为具有相同大小的两个矩阵的相应分量的乘积之和。

对张量的泛化

一个n阶的张量和一个m阶的张量之间的点积是一个n+m-2阶的张量。点积是通过在两个张量中的一个索引上进行相乘和计算出来的。如果A {displaystyle mathbf {A}} $\mathbf {A}$ 和 B {displaystyle\mathbf {B}.} $\mathbf {B}$ 是两个张量，其元素表示为A i j ... k ℓ ... {displaystyle A_{ij\dots }^{kell\dots } $A_{ij\dots }^{k\ell \dots }$ 和 B m n ... p ... i {displaystyle B_{mn\dots }^{p{\dots }i}} $B_{mn\dots }^{p{\dots }i}$ ，点积A⋅B的元素 {displaystyle \mathbf {A}} 。\cdot \mathbf {B}的元素。} $\mathbf {A} \cdot \mathbf {B}$ 是由以下公式给出的

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ... B m n ... p ...i {displaystyle A_{ij\dots }^{kell\dots }B_{mn\dots }^{p{dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{kell\dots }B_{mn\dots }^{p{dots }i}。 $A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}$

这个定义在应用于向量时，自然可以简化为标准的向量点积，在应用于矩阵时，可以简化为矩阵乘法。

偶尔，双点积被用来表示跨两个索引的乘法和。两个二阶张量之间的双点积是一个标量。

问题和答案

问：什么是数学中的点积？
答：点积是将两个向量作为输入，并将一个标量数作为输出返回的运算。

问：点积取决于什么？
答：点积取决于两个向量的长度和它们之间的夹角。

问：为什么点积的名称源自居中的点"-"？
答：点积的名称来源于居中的点"-"，它经常被用来表示这一运算。

问：点积的另一个名称是什么？
答：另一个名称是标量积，它强调结果的标量（而不是矢量）性质。

问：在三维空间中，点积和叉积有什么不同？
答：点积的结果是标量，而交积的结果是矢量。

问：点积在数学中的用途是什么？
答：点积可用于确定两个向量是否垂直（角度为 90 度），以及将一个向量投影到另一个向量上。

问：点积可以用于高维空间吗？
答：可以，点积可以通过概括定义扩展到高维空间。

点积

定义