分子轨道
在化学中,分子轨道(或称MO)解释了当原子在分子中结合在一起时电子会发生什么。分子轨道是一个数学函数,它描述了电子在分子中的波状行为,化学家用这种函数来预测或解释化学和物理性质。化学家利用这些函数来预测或解释化学和物理性质。例如,这些函数可以知道在任何特定区域找到电子的概率。
化学家通常通过组合原子轨道来建立分子轨道的数学模型。也可以使用分子中每个原子的混合轨道,或其他原子组的分子轨道。计算机可以在这些功能上工作。分子轨道允许化学家应用量子力学来研究分子。分子轨道回答了关于分子中的原子如何粘在一起的问题。在轨道图中,各种圆形的形状表示电子最可能出现在原子中的位置。
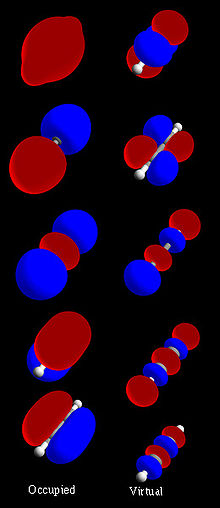
图1:完整的乙炔(H-C≡C-H)分子轨道组。
历程
轨道一词最早是由罗伯特-S-穆利肯在英文中使用的。德国物理学家Erwin Schrödinger更早地写过MOs。薛定谔称它们为Eigenfunktion。
物理学家马克斯-博恩在1926年描述了分子轨道背后的理论,今天,它被称为博恩规则,是哥本哈根解释量子力学的一部分。今天,它被称为博恩规则,是量子力学哥本哈根解释的一部分。当初提出时,这个理论与尼尔斯-玻尔的原子模型不一致。玻尔的模型描述了电子作为"轨道"的核,因为他们在圆周移动。然而,博恩模型最终获得了大众的支持,因为它能够描述电子在分子内的位置,并解释了一些以前无法解释的化学反应。
概述
原子轨道预测电子在原子中的位置。当原子轨道结合在一起时,就会产生分子轨道。分子轨道可以提供有关分子电子构型的信息。电子构型是一个(或一对)电子最可能的位置和能量。大多数情况下,MO被表示为原子轨道的线性组合(LCAO-MO法),尤其是在近似使用中。这意味着化学家假设一个电子在分子中任何一点的机会是基于单个原子轨道的电子在那里的概率之和。LCAO-MO是分子中键合的简单模型,对于研究分子轨道理论具有重要意义。
理论化学家用计算机来计算不同分子(包括真实的和虚构的)的MO。计算机可以绘制"云"的图形,以显示电子在任何区域的可能性。计算机还可以提供有关分子的物理性质的信息。它们还可以说出形成分子需要多少能量。这有助于化学家说一些小分子是否可以结合起来形成更大的分子。
目前大多数计算化学的方法都是从计算一个系统的MO开始的。每个MO的电场是由所有原子核和其他电子的一些平均分布产生的。
类比
理解MOs就像了解一个大型家装店中每个员工的位置一样(不用看店内的情况)。分析师知道在商店工作的员工人数和每个员工的部门。他还知道员工之间不会互相踩踏,员工站在过道上而不是商品货架上。员工离开自己的部门是为了帮助顾客找到其他部门的商品或检查库存。分析师在不看店内情况的情况下,给出选定时刻店内所有员工的位置,就像化学家计算分子的MOs一样。正如MOs不能告诉每个电子的确切位置一样,每个员工的确切位置也不知道。一个MO有一个节点平面,就像员工走在过道上而不是穿过货架的结论一样。虽然电子是由一个特定的原子贡献出来的,但电子填满一个MO而不考虑它的源原子。这就像员工白天离开自己的部门去商店的其他地方行走一样。所以,MO是对电子的不完全描述,就像分析师对看不见的商店的计算是对员工位置的不完全猜测一样。

计算MOs就像预测家装店中每个员工的位置一样。
分子轨道的形成
理论化学家已经发明了计算MOs的规则。这些规则来自于对量子力学的理解。量子力学帮助化学家利用物理学关于电子的说法来计算电子在分子中的行为。分子轨道是由原子轨道之间"允许的"相互作用形成的。(如果原子轨道的对称性(由群论决定)相互兼容,那么这种相互作用就是"允许的")。化学家研究原子轨道相互作用。这些相互作用来自于两个原子轨道之间的重叠(衡量两个轨道之间建设性相互作用的程度)。如果原子轨道的能量很接近,那么重合度就很重要。最后,一个分子中MO的数量必须等于被聚集在一起形成分子的原子轨道的数量。
定性方法
化学家需要了解MOs的几何学,才能讨论分子结构。LCMO(线性组合原子轨道分子轨道)方法对MOs给出了一个粗略但很好的描述。在这种方法中,分子轨道被表示为分子中每个原子的所有原子轨道的线性组合。
原子轨道的线性组合(LCAO)
分子轨道最早由弗里德里希-亨德和罗伯特-S-穆利肯于1927年和1928年提出。
原子轨道的线性组合或分子轨道的"LCAO"近似是由John Lennard-Jones爵士在1929年提出的。他的开创性论文显示了如何从量子原理推导出氟和氧分子的电子结构。这种分子轨道理论的定性方法是现代量子化学的开端之一。
原子轨道的线性组合(LCAO)可以用来猜测分子的原子结合在一起时的分子轨道。与原子轨道类似,描述电子行为的薛定谔方程也可以构建分子轨道。原子轨道的线性组合,(原子波函数的和与差)提供了分子薛定谔方程的近似解。对于简单的二原子分子,你得到的波函数在数学上用方程来表示
Ψ = caψa + cbψb
和
Ψ* = caψa - cbψb
其中Ψ和Ψ*分别是成键和反键分子轨道的分子波函数,ψa和ψb分别是来自原子a和b的原子波函数,ca和cb是可调系数。这些系数可以是正的或负的,取决于各个原子轨道的能量和对称性。当两个原子的距离越来越近时,它们的原子轨道就会重叠,产生高电子密度的区域。所以,两个原子之间就形成了分子轨道。带正电的原子核和占据键合分子轨道的带负电的电子之间的静电吸引将原子固定在一起。
粘结、反粘结和非粘结性MOs
当原子轨道发生相互作用时,产生的分子轨道可以有三种类型:成键、反成键或非成键。
粘合MOs。
- 原子轨道间的键合作用属于建构(相位)作用。
- 键合MOs的能量比结合产生它们的原子轨道要低。
抗粘结性MOs。
- 原子轨道间的反键作用是破坏性(相外)作用。
- 反键MOs的能量高于结合产生它们的原子轨道。
非粘结性MOs。
- 非键合MOs是由于原子轨道之间没有相互作用,因为缺乏相容的对称性。
- 非键合MO将具有与分子中某一原子的原子轨道相同的能量。
HOMO和LUMO
每个分子轨道都有自己的能级。化学家按能级对分子轨道进行排序。化学家假设电子将首先填满能级最低的MOs。例如,如果一个分子有电子可以填满15个轨道,那么15个能级最低的MO将被填满。列表中的第15个MO将被称为"最高占用的分子轨道"(HOMO),列表中的第16个MO将是"最低未占用的分子轨道"(LUMO)。HOMO的能级与LUMO的能级之差称为带隙。带隙有时可以作为衡量分子可激发性的标准:能量越小,越容易被激发。当电子被激发时,它将跳到一个未被占据的MO上。例如,这可以帮助猜测某物是否会发出光(发光)。
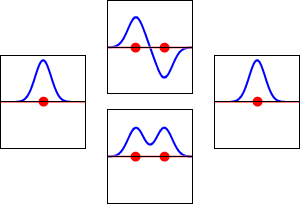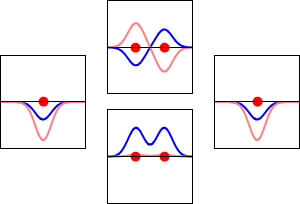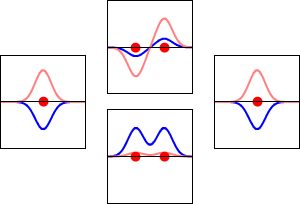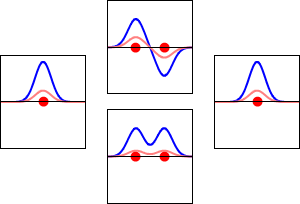
氢原子的1s轨道(左、右)和H2分子相应的成键(下)和反键(上)分子轨道的电子波函数。波函数的实部是蓝色曲线,虚部是红色曲线。红点标志着质子的位置。电子波函数根据薛定谔波方程振荡,轨道是其驻波。驻波频率与轨道的能量成正比。此图是三维系统的一维切片)。
问题和答案
问:什么是分子轨道?答:分子轨道(或MO)是一个数学函数,描述了分子中电子的波状行为。它解释了当原子在分子中结合在一起时,电子会发生什么变化,并能说明在任何特定区域找到电子的概率。
问:化学家是如何建立分子轨道的数学模型的?
答:化学家通常通过结合原子轨道来建立分子轨道的数学模型。也可以使用来自分子中每个原子的混合轨道,或来自原子组的其他分子轨道。计算机可以在这些函数上工作。
问:量子力学与研究分子有什么关系?
答:分子轨道使化学家能够应用量子力学来研究分子。它们回答了关于分子中的原子如何粘在一起的问题,并提供了对化学和物理特性的洞察力。
问:什么是轨道图?
答:轨道图是一种视觉表现,它根据原子的各种圆形表明电子最可能出现的位置。
问:混合轨道是如何工作的?
答:混合轨道将不同类型的原子轨道组合成一种新的类型,与它的组成部分相比具有独特的特性。这些混合轨道在建立分子轨道的数学模型时经常被使用。
问:计算机如何帮助研究MO?
答:计算机可以通过研究MOs的功能,为分子内的化学和物理性质提供更准确的预测或解释,从而帮助研究MOs。
搜索百科全书