表面积分

在数学中，曲面积分是指在一个曲面（可能是空间中的一个曲线集）上的定积分。就像直线积分处理一个维度或一个变量一样，曲面积分可以被认为是沿两个维度的双重积分。给定一个曲面，我们可以对其标量场（即以数字为数值的函数）和矢量场（即以矢量为数值的函数）进行积分。

表面积分在物理学上有应用，特别是与电磁学的经典理论。

表面积分的定义依赖于将表面分割成小的表面元素。

一个单一的表面元素的插图。这些元素通过限制过程变得无限小，以便与表面相近。

标量场的表面积分

考虑一个表面S，其上定义了一个标量场f。如果我们认为S是由某种材料构成的，对于S中的每个x，数字f(x)是x处的材料密度，那么f在S上的表面积分就是S的每单位厚度的质量。计算表面积分的一种方法是将表面分成许多小块，假设每块上的密度近似恒定，用每块的密度乘以它的面积，求出每块的单位厚度的质量，然后将所得数字相加，求出S的单位厚度的总质量。

为了找到表面积分的明确公式，数学家通过在S上考虑一个曲线坐标系统来对S进行参数化，就像球体上的纬度和经度。让这样的参数化为x(s, t)，其中(s, t)在平面的某个区域T内变化。那么，表面积分由以下公式给出

∫ S f d S = ∫ T f ( x ( s , t ) )| ∂ x ∂ s × ∂ x ∂ t | d s d t {displaystyle int _{S}f\,dS=iint _{T}f(\mathbf {x} (s,t))\left|{partial \mathbf {x}} 次\over `partial s`times {partial `mathbf {x}(s,t)\over /partial t}right|ds\,dt}。 $\int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt$

其中右侧条形之间的表达式是x(s, t)的偏导数的交叉积的大小。

例如，要找到一些一般的函数形状的表面积，例如z = f ( x , y ) {displaystyle z=f\,(x,y)} $z=f\,(x,y)$ ，我们有

A = ∫ S d S = ∫ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {displaystyle A=int _{S}\,dS=iint _{T}\left\|{partial \mathbf {r}}.\over `partial x `times {partial `mathbf {r `}.\over y}right\|dx\,dy}。 $A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy$

其中r = ( x , y , z ) = ( x , y , f ( x , y ) ){displaystyle\mathbf {r}=(x,y,z)=(x,y,f(x,y))} $\mathbf {r} =(x,y,z)=(x,y,f(x,y))$ 。因此，∂r ∂x = ( 1 , 0 , f x ( x , y ) ){displaystyle {partial\mathbf {r}.\1,0,f_{x}(x,y))}。 ${\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))$ 而 ∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ){displaystyle {partial\mathbf {r} {displaystyle {partial\mathbf {r} {displaystyle∂ y=(0,1,f_{y}(x,y))} ${\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))$ 。所以。

A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle{\begin{aligned}A&{}==iint _{T}\left\|left(1,0,{\partial f\over \partial x}right)\times \left(0,1,{\partial f\over \partial y}right)\right|dx,dy\&。{}=iint _{T}\left\|left(-{partial f\over \partial x},-{partial f\over \partial y},1\right)\right\|dx,dy\&。{}==iint _{T}{sqrt {left({partial f\over partial x}\right)^{2}+\left({partial f\over partial y}\right)^{2}+1}}\,dx\,dy\end{aligned}}。 ${\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,dx\,dy\end{aligned}}$

这是用于计算一般函数形状的表面积的公式。人们可以认识到上面第二行的矢量是表面的法向量。

请注意，由于交叉积的存在，上述公式只对嵌入三维空间的曲面有效。

矢量场的表面积分

考虑S上的一个矢量场v，也就是说，对于S中的每个x，v(x)是一个矢量。

表面积分可以根据标量场的表面积分的定义来定义分量，其结果是一个矢量。例如，这适用于某个固定点由于带电表面而产生的电场，或者某个固定点由于材料片而产生的重力。它还可以计算通过一个表面的磁通量。

另外，数学家可以对矢量场的法向分量进行积分，其结果是一个标量。一个例子是流经S的流体，如v(x)决定了流体在x处的速度。流量被定义为单位时间内流经S的流体数量。

这个插图意味着，如果矢量场在每一点上都与S相切，那么通量就是零，因为流体只是平行于S流动，既不流入也不流出。这也意味着，如果v不只是沿S流动，也就是说，如果v既有切向分量又有法向分量，那么只有法向分量对通量有贡献。基于这一推理，为了找到通量，我们需要在每一点上取v与S的单位表面法线的点积，这将给我们一个标量场，并按上述方法对得到的场进行积分。这就给出了一个公式

∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∫ T v ( x ( s , t ) )⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t 。{displaystyle {int _{S}{mathbf {v}}\cdot\,d{mathbf {S}}=int _{S}{mathbf {v}}。}=int _{S}({mathbf {v} }\cdot {mathbf {n} }),ds=iint _{T}{mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x})\over `partial s`times {partial `mathbf {x`}(s,t)\over \partial t \right）ds\,dt.} $\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt.$

这个表达式右边的交叉积是由参数化决定的表面法线。

这个公式定义了左边的积分（注意点和表面元素的向量符号）。

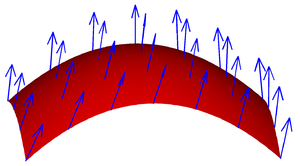
一个表面上的矢量场。

涉及表面积分的定理

利用微分几何和矢量微积分可以得出各种有用的表面积分结果，如发散定理及其推广，斯托克斯定理。

高级问题

改变参数化

上面的讨论是通过使用曲面S的参数化来定义曲面积分的，一个特定的曲面可能有几个参数化。例如，当北极和南极的位置在一个球体上移动时，球体上所有的点的经纬度都会改变。那么，一个自然的问题是，表面积分的定义是否取决于所选择的参数化。对于标量场的积分，这个问题的答案很简单，无论使用何种参数化，表面积分的值都是一样的。

矢量场的积分则更为复杂，因为涉及到表面法线。数学家们已经证明，给定同一表面的两个参数，其表面法线指向同一方向，两个参数给出的表面积分值是相同的。然而，如果这些参数化的法线指向相反的方向，那么用一种参数化得到的曲面积分值就是用另一种参数化得到的积分值的负数。由此可见，给定一个曲面，我们不需要坚持任何唯一的参数化；但是，在整合矢量场时，我们确实需要事先决定法线将指向哪个方向，然后选择与该方向一致的任何参数化。

参数化对部分表面的工作

另一个问题是，有时曲面没有覆盖整个表面的参数；例如圆柱体的表面（高度有限）就是如此。明显的解决办法是把这个表面分成几块，在每一块上计算表面积分，然后把它们全部加起来。这确实是工作的方式，但在对矢量场进行积分时，需要再次注意如何为每一块表面选择法线指向的矢量，这样当这些部分重新组合起来时，结果是一致的。对于圆柱体来说，这意味着如果我们决定侧面区域的法线将指向体外，那么对于顶部和底部的圆形部分，法线也必须指向体外。

不一致的表面法线

最后，有些曲面在每一点上都没有一致的表面法线（例如莫比乌斯带）。如果这样的曲面被分割成几块，在每块上选择一个参数和相应的曲面法线，然后把这几块重新组合起来，来自不同的几块的法线向量就不能调和。这意味着，在两块面之间的某个交界处，法向量会指向相反的方向。这样的表面被称为非定向的。向量场不能在非定向表面上进行积分。